
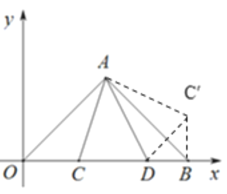
【题目】如图,在平面直角坐标系中,点B在x轴的正半轴上,AO=AB,∠OAB=90°,OB=12,点C、D均在边OB上,且∠CAD=45°,若△ACO的面积等于△ABO面积的![]() ,则点D的坐标为 _______ 。
,则点D的坐标为 _______ 。

【答案】(9,0)
【解析】
将△AOC绕点A逆时针旋转,使得AO和AB重合,构造出直角三角形,利用旋转的性质证明全等,通过勾股定理设出未知数列方程求解.
解:将△AOC绕点A逆时针旋转,使得AO和AB重合,旋转后点C到点C′的位置,连接C′D,
∵AO=AB,∠OAB=90°,
∴△AOB为等腰直角三角形,
∵∠CAD=45°,
∴∠C′AD=45°,
又∵AC=AC′,AD=AD
∴△ACD≌△AC′D(SAS)
∴CO=CD′
∵若△ACO的面积等于△ABO面积的![]() ,OB=12,
,OB=12,
∴OC= BC′=4,BC=8,
∵∠AOC=∠AB C′=45°,∠ABO=45°
∴∠C′BO=90°,
设CD=x,在Rt△DBC′中,
C′D2=BD2+BC′2,
解得:x=5,
即CD=5,
∵OC=4,
所以OD=9,
∴D(9,0)


科目:初中数学 来源: 题型:
【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y(元),生产A产品x(件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?画出图形,写出结论不证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
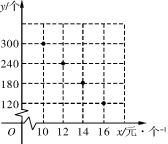
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量![]() (单位:个)与销售单价
(单位:个)与销售单价![]() (单位:元/个)之间的对应关系如图所示:
(单位:元/个)之间的对应关系如图所示:
(1) ![]() 与
与![]() 之间的函数关系是 .
之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润![]() (单位:元)与销售单价
(单位:元)与销售单价![]() (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四边形![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 、
、![]() 的中点,请添加一个与四边形
的中点,请添加一个与四边形![]() 对角线有关的条件________,使四边形
对角线有关的条件________,使四边形![]() 是特殊的平行四边形为________形.
是特殊的平行四边形为________形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC是等边三角形,D是BC的中点,以点D为旋转中心,把△ABC顺时针旋转60°后所成的图形应是下图(注:虚线代表三角形原来的位置,实线代表旋转后的位置)中的( ).

A. ![]() B.
B.  C.
C.  D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=ax2+bx+c(a≠0)的顶点是(1,4),且图象过点A(3,0),与y轴交于点B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)求直线AB的解析式;
(3)在直线AB上方的抛物线上是否存在一点C,使得S△ABC=![]() .如果存在,请求出C点的坐标;如果不存在,请说明理由.
.如果存在,请求出C点的坐标;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com