
已知:如图,△ABC中,AD是BC边上的中线,四边形ABDE是平行四边形
(1)求证:四边形ADCE是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCE是菱形?说明你的理由.
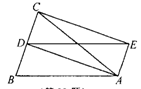
(1)见解析(2)当△ABC满足∠BAC=90°时,四边形ADCE是菱形,理由见解析
解析:(1)证明:∵四边形ABDE是平行四边形,
∴BD∥AE,BD=AE. …………………………1分
∵△ABC中,AD是BC边上的中线
∴BD=CD.
∴CD=AE. …………………………2分
又∵CD∥AE,∴四边形ADCE是平行四边形. ………3分
(2)解:当△ABC满足∠BAC=90°时,四边形ADCE是菱形.……………………4分
∵△ABC中,∠BAC=90°,BD=CD.
∴AD=CD. ……………………5分
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形. ……………………6分
证明是平行四边形的方法有很多,此题用一组对边平行且相等较为简单,在平行四边形的基础上只需邻边相等即可证出菱形


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
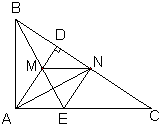 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
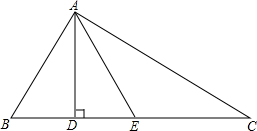 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com