
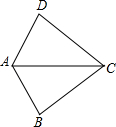
 如图,已知∠DAC=∠BAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知∠DAC=∠BAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A. | AB=AD | B. | ∠BCA=∠DCA | C. | CB=CD | D. | ∠ADC=∠ABC |
分析 全等三角形的判定定理有SAS,ASA,AAS,SSS,根据以上内容判断即可.
解答 解:A、∵在△ABC和△ADC中
$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAC}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC(SAS),正确,故本选项错误;
B、∵在△ABC和△ADC中
$\left\{\begin{array}{l}{∠BAC=∠DAC}\\{AC=AC}\\{∠BCA=∠DCA}\end{array}\right.$,
∴△ABC≌△ADC(ASA),正确,故本选项错误;
C、根据CB=CD,AC=AC,∠BAC=∠DAC,不能推出△BAC和△DAC全等,错误,故本选项正确;
D、∵在△ABC和△ADC中
$\left\{\begin{array}{l}{∠ABC=∠ADC}\\{∠BAC=∠DAC}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC(AAS),正确,故本选项错误;
故选C.
点评 本题考查了全等三角形的判定,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
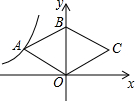 如图,菱形OABC的顶点O是原点,点B在y轴正半轴上,函数y=-$\frac{6}{x}$(x<0)的图象经过点A,则菱形OABC的面积为12.
如图,菱形OABC的顶点O是原点,点B在y轴正半轴上,函数y=-$\frac{6}{x}$(x<0)的图象经过点A,则菱形OABC的面积为12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
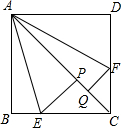 如图,在正方形ABCD内,以A为顶点作∠EAF=45°.设这个角的两边分别交正方形的边BC、CD于E、F,自E、F分别作正方形AC的垂线,垂足为P、Q.求证:过B、P、Q所作的圆的圆心在BC上.
如图,在正方形ABCD内,以A为顶点作∠EAF=45°.设这个角的两边分别交正方形的边BC、CD于E、F,自E、F分别作正方形AC的垂线,垂足为P、Q.求证:过B、P、Q所作的圆的圆心在BC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
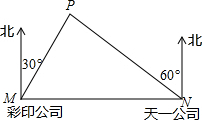 如图,我市计划在某工业园区内,为相距4千米的彩印公司、天一公司修一条笔直的公路,在彩印公司北偏东30°方向与天一公司北偏西60°方向的交点处,有一个以P为圆心,0.8千米为半径区域的住宅小区,问这条公路是否会穿越这个住宅小区?(参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}≈1.732$)
如图,我市计划在某工业园区内,为相距4千米的彩印公司、天一公司修一条笔直的公路,在彩印公司北偏东30°方向与天一公司北偏西60°方向的交点处,有一个以P为圆心,0.8千米为半径区域的住宅小区,问这条公路是否会穿越这个住宅小区?(参考数据:$\sqrt{2}≈1.414$,$\sqrt{3}≈1.732$)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
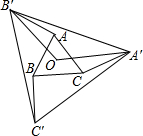 如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB'、BC'、CA',连接A'B'、B'C'、A'C'、
如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB'、BC'、CA',连接A'B'、B'C'、A'C'、查看答案和解析>>
科目:初中数学 来源: 题型:解答题
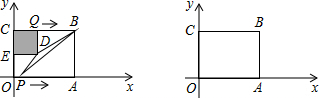
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
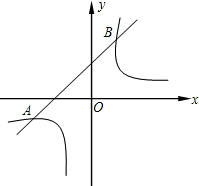 如图,已知双曲线y=$\frac{12}{x}$与直线y=x+1交于点A、B两点
如图,已知双曲线y=$\frac{12}{x}$与直线y=x+1交于点A、B两点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com