
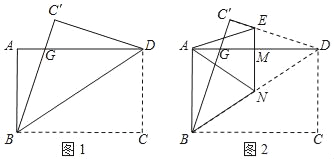
【题目】一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,使点C落在点C′的位置,BC′交AD于点G(图1);再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M(图2),则EM的长为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析: (1)通过证明△GAB≌△GC′D即可证得线段AG、C′G相等;
(2)在直角三角形DMN中,利用勾股定理求得MN的长,则EN-MN=EM的长.
详解: (1)证明:∵沿对角线BD对折,点C落在点C′的位置,
∴∠A=∠C′,AB=C′D
∴在△GAB与△GC′D中,

∴△GAB≌△GC′D
∴AG=C′G;
(2)∵点D与点A重合,得折痕EN,
∴DM=4cm,
∵AD=8cm,AB=6cm,
在Rt△ABD中,BD=![]() =10cm,
=10cm,
∵EN⊥AD,AB⊥AD,
∴EN∥AB,
∴MN是△ABD的中位线,
∴DN=![]() BD=5cm,
BD=5cm,
在Rt△MND中,
∴MN=![]() =3(cm),
=3(cm),
由折叠的性质可知∠NDE=∠NDC,
∵EN∥CD,
∴∠END=∠NDC,
∴∠END=∠NDE,
∴EN=ED,设EM=x,则ED=EN=x+3,
由勾股定理得ED=EM+DM,即(x+3) =x+4,
解得x=![]() ,即EM=
,即EM=![]() cm.
cm.
点睛: 本题考查了折叠的性质,三角形全等的判定与性质,三角形相似的判定与性质,勾股定理的运用.关键是由性质将有关线段进行转化.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 、
、![]() 轴于点A、B两点,OA=5,∠OAB=60°.
轴于点A、B两点,OA=5,∠OAB=60°.
(1)如图1,求直线AB的解析式;
(2)如图2,点P为直线AB上一点,连接OP,点D在OA延长线上,分别过点P、D作OA、OP的平行线,两平行线交于点C,连接AC,设AD=m,△ABC的面积为S,求S与m的函数关系式;
(3)如图3,在(2)的条件下,在PA上取点E ,使PE=AD, 连接EC,DE,若∠ECD=60°,四边形ADCE的周长等于22,求S的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
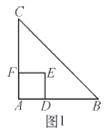
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,点D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF; ②当AB=4,AD=![]() 时,求线段BG的长.
时,求线段BG的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与反比例函
,与反比例函![]() 的图象交于点
的图象交于点![]() ,且
,且![]() .
.
(1)求点![]() 的坐标和反比例函数
的坐标和反比例函数![]() 的解析式;
的解析式;
(2)点![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() 图象上存在点
图象上存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形,求点M的坐标.
为平行四边形,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列语句画图:
(1)画∠AOB=120°;
(2)画∠AOB的角平分线OC;
(3)反向延长OC得射线OD;
(4)分别在射线OA、OB、OD上画线段OE=OF=OG=2cm;
(5)连接EF、EG、FG;
(6)你能发现EF、EG、FG有什么关系?∠EFG、∠EGF、∠GEF有什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房成交均价由今年3月份的14 000元/m2下降到5月份的12 600元/m2.
(1)问4,5两月平均每月降价的百分率约是多少?(参考数据:![]() ≈0.95)
≈0.95)
(2)如果房价继续跌落,按此降价的百分率,你预测到7月份该市的商品房成交均价是否会跌跛10 000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区. 已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com