
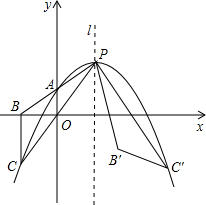
 如图,抛物线y=a(x-m)2+2m-2(其中m>1)顶点为P,与y轴相交于点A(0,m-1).连接并延长PA、PO分别与x轴、抛物线交于点B、C,连接BC,将△PBC绕点P逆时针旋转得△PB′C′,使点C′正好落在抛物线上.
如图,抛物线y=a(x-m)2+2m-2(其中m>1)顶点为P,与y轴相交于点A(0,m-1).连接并延长PA、PO分别与x轴、抛物线交于点B、C,连接BC,将△PBC绕点P逆时针旋转得△PB′C′,使点C′正好落在抛物线上.分析 (1)只需将A点坐标(0,m-1)代入y=a(x-m)2+2m-2,即可求出a值,从而得到抛物线的解析式.
(2)由点A、P的坐标可求出直线AP的解析式,从而求出点B的横坐标为-m;由点P的坐标可求出直线OP的解析式,从而求出直线OP与抛物线的交点C的横坐标为-m.由于点B、C的横坐标相同,故BC∥y轴.
(3)利用三角形的内角和定理、图形旋转的性质等知识,结合条件可以证到∠POD=∠BAO,从而可以证到△BAO∽△POD,进而得到$\frac{BO}{PD}=\frac{AO}{OD}$,由BO=m,PD=2m-2,AO=m-1,OD=m,可得:$\frac{m}{2m-2}=\frac{m-1}{m}$,通过解方程就可解决问题.
解答 (1)解:∵A(0,m-1)在抛物线y=a(x-m)2+2m-2上,
∴a(0-m)2+2m-2=m-1.
∴a=$\frac{1-m}{{m}^{2}}$.
∴抛物线的解析式为y=$\frac{1-m}{{m}^{2}}$(x-m)2+2m-2.
故答案为:y=$\frac{1-m}{{m}^{2}}$(x-m)2+2m-2.
(2)证明:如图1,
设直线PA的解析式为y=kx+b,
∵点P(m,2m-2),点A(0,m-1).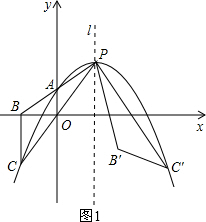
∴$\left\{\begin{array}{l}{mk+b=2m-2}\\{b=m-1}\end{array}\right.$.
解得:$\left\{\begin{array}{l}{k=\frac{m-1}{m}}\\{b=m-1}\end{array}\right.$.
∴直线PA的解析式是y=$\frac{m-1}{m}$x+m-1.
当y=0时,$\frac{m-1}{m}$x+m-1=0.
∵m>1,
∴x=-m.
∴点B的横坐标是-m.
设直线OP的解析式为y=k′x,
∵点P的坐标为(m,2m-2),
∴k′m=2m-2.
∴k′=$\frac{2m-2}{m}$.
∴直线OP的解析式是y=$\frac{2m-2}{m}$x.
联立$\left\{\begin{array}{l}{y=\frac{2m-2}{m}x}\\{y=\frac{1-m}{{m}^{2}}(x-m)^{2}+2m-2}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=m}\\{y=2m-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-m}\\{y=2-2m}\end{array}\right.$.
∵点C在第三象限,且m>1,
∴点C的横坐标是-m.
∴BC∥y轴.
(3)方法一:
解:若点B′恰好落在线段BC′上,
设对称轴l与x轴的交点为D,连接CC′,如图2,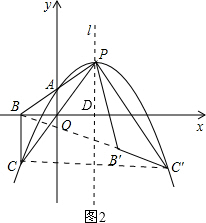
则有∠PB′C′+∠PB′B=180°.
∵△PB′C′是由△PBC绕点P逆时针旋转所得,
∴∠PBC=∠PB′C′,PB=PB′,∠BPB′=∠CPC′.
∴∠PBC+∠PB'B=180°.
∵BC∥AO,
∴∠ABC+∠BAO=180°.
∴∠PB′B=∠BAO.
∵PB=PB′,PC=PC′,
∴∠PB′B=∠PBB′=$\frac{180°-∠BPB'}{2}$,
∴∠PCC′=∠PC′C=$\frac{180°-∠CPC'}{2}$.
∴∠PB′B=∠PCC′.
∴∠BAO=∠PCC′.
∵点C关于直线l的对称点为C′,
∴CC′⊥l.
∵OD⊥l,
∴OD∥CC′.
∴∠POD=∠PCC′.
∴∠POD=∠BAO.
∵∠AOB=∠ODP=90°,∠POD=∠BAO,
∴△BAO∽△POD.
∴$\frac{BO}{PD}=\frac{AO}{OD}$.
∵BO=m,PD=2m-2,AO=m-1,OD=m,
∴$\frac{m}{2m-2}=\frac{m-1}{m}$.
解得:
∴m1=2+$\sqrt{2}$,m2=2-$\sqrt{2}$.
经检验:m1=2+$\sqrt{2}$,m2=2-$\sqrt{2}$都是分式方程的解.
∵m>1,
∴m=2+$\sqrt{2}$.
∴若点B′恰好落在线段BC′上,此时m的值为2+$\sqrt{2}$.
方法二:
∵点C关于直线l的对称点为C″,
∴Px=$\frac{{C}_{X}+C{'}_{X}}{2}$,
∵C(-m,2-2m),P(m,2m-2),
∴m=$\frac{-m+C{'}_{x}}{2}$,
∴C′X=3m,
∴C′(3m,2-2m),
∵将△PBC绕点P逆时针旋转,
∴△BCP≌△B′C′P,
∵点B′恰好落在线段BC′上,
∴线段BP所对的∠BCP=∠B′C′P,
∴点P,B,C,C′四点共圆,(同侧共底的两个三角形顶角相等,则四点共圆)
∵CY=C′Y=2-2m,
∴CC′⊥BC,
∴BC′为P,B,C,C′四点共圆所在圆的直径,
∴BP⊥C′P,
∴KBP×KC′P=-1,
∵P(m,2m-2),
∴C′(3m,2-2m),B(-m,0),
∴$\frac{2m-2-2+2m}{m-3m}×\frac{2m-2}{m+m}=-1$=-1,
∴m2-4m+2=0,
∴m1=2-$\sqrt{2}$,m2=2+$\sqrt{2}$,
∵m>1,
∴m=2+$\sqrt{2}$.
点评 本题考查了用待定系数法求二次函数及一次函数的解析式、相似三角形判定与性质、平行线的判定与性质、等腰三角形的性质、解分式方程、三角形的内角和定理、旋转的性质、抛物线与直线的交点等知识,综合性比较强,有一定的难度.而证明∠POD=∠BAO,进而证到△BAO∽△POD是解决第3小题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
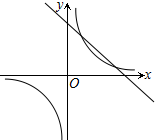 已知双曲线y=$\frac{6}{x}$和直线y=kx+4.
已知双曲线y=$\frac{6}{x}$和直线y=kx+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com