
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象与x轴的相交情况,关于下列结论:
①方程ax2+bx=0的两个根为x1=0,x2=﹣4;②b﹣4a=0;③9a+3b+c<0;其中正确的结论有( )
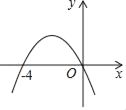
A. 0个B. 1个C. 2个D. 3个
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
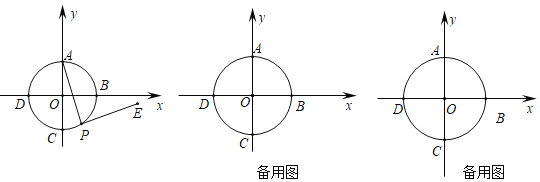
【题目】如图,半径为4且以坐标原点为圆心的圆O交x轴,y轴于点B、D、A、C,过圆上的动点![]() 不与A重合
不与A重合![]() 作
作![]() ,且
,且![]() 在AP右侧
在AP右侧![]() .
.
![]() 当P与C重合时,求出E点坐标;
当P与C重合时,求出E点坐标;
![]() 连接PC,当
连接PC,当![]() 时,求点P的坐标;
时,求点P的坐标;
![]() 连接OE,直接写出线段OE的取值范围.
连接OE,直接写出线段OE的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
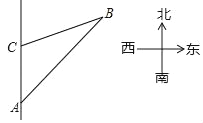
【题目】一艘货轮以36km/h的速度在海面上沿正北方向航行,当行驶至A处时,发现北偏东37°方向有一个灯塔B,货轮继续向北航行20分钟后到达C处,发现灯塔B在它的北偏东67°方向,则此时货轮与灯塔B的距离为_____km.(结果精确到0.1,参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin67°≈0.920,cos67°≈0.391,tan67°≈2.356)
查看答案和解析>>
科目:初中数学 来源: 题型:
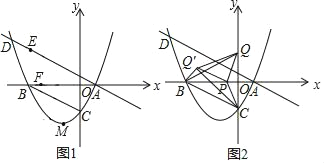
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A,B两点,交y轴于点C,连接BC.过点A作BC的平行线交抛物线于点D.
与x轴交于A,B两点,交y轴于点C,连接BC.过点A作BC的平行线交抛物线于点D.
(1)求△ABC的面积;
(2)已知点M是抛物线的顶点,在直线AD上有一动点E,x轴上有一动点F,当ME+BE最小时,求|CF﹣EF|的最大值及此时点F的坐标;
(3)如图2,在y轴正半轴上取点Q,使得CB=CQ,点P是x轴上一动点,连接PC,将△CPQ沿PC折叠至△CPQ′.连接BQ,BQ′,QQ′,当△BQQ′为等腰三角形时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3![]() ;其中正确的结论是( )
;其中正确的结论是( )

A. ①②③ B. ①③④ C. ②③④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )

④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
查看答案和解析>>
科目:初中数学 来源: 题型:
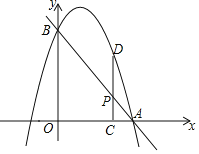
【题目】如图,已知直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC
轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC![]()
![]() 轴于点C,交抛物线于点D.
轴于点C,交抛物线于点D.
(1)若抛物线的解析式为![]() ,设其顶点为M,其对称轴交AB于点N.
,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与![]() AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com