

 ,
, ×3×
×3× =
=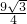 ,
,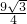 -S△AEF,
-S△AEF, ,S△AEF=
,S△AEF= ×
× ×
× =
= ,
,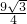 -S△AEF═
-S△AEF═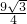 -
- =
=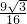 ;
; ,
, ,
, PD,PN=
PD,PN= PD,
PD, =PD+
=PD+ PD+
PD+ PD,
PD, -3;
-3;
 ,
, PD,
PD, =PD+2PD+
=PD+2PD+ PD,
PD,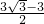 .
.

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
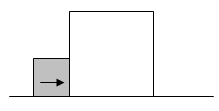
已知,大正方形的边长为4![]() ,小正方形的边长为2
,小正方形的边长为2![]() ,状态如图所示.大正方形固定不动,把小正方形以
,状态如图所示.大正方形固定不动,把小正方形以![]() 的速度向大正方形的内部沿直线平移,设平移的时间为
的速度向大正方形的内部沿直线平移,设平移的时间为![]() 秒,两个正方形重叠部分的面积为
秒,两个正方形重叠部分的面积为![]()
![]() ,完成下列问题:
,完成下列问题:
1.用含![]() 的式子表示
的式子表示![]() ,要求画出相应的图形,表明
,要求画出相应的图形,表明![]() 的范围;
的范围;
2.当![]() ,求重叠部分的面积
,求重叠部分的面积![]() ;
;
3.当![]()
![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2011届大连市七年级(下)数学月考卷 题型:解答题
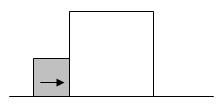
已知,大正方形的边长为4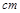 ,小正方形的边长为2
,小正方形的边长为2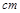 ,状态如图所示.大正方形固定不动,把小正方形以
,状态如图所示.大正方形固定不动,把小正方形以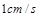 的速度向大正方形的内部沿直线平移,设平移的时间为
的速度向大正方形的内部沿直线平移,设平移的时间为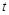 秒,两个正方形重叠部分的面积为
秒,两个正方形重叠部分的面积为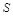
 ,完成下列问题:
,完成下列问题:
【小题1】用含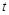 的式子表示
的式子表示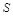 ,要求画出相应的图形,表明
,要求画出相应的图形,表明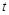 的范围;
的范围;
【小题2】当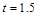 ,求重叠部分的面积
,求重叠部分的面积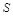 ;
;
【小题3】当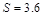
 ,求
,求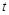 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2011年大连市七年级(下)数学月考卷 题型:解答题
已知,大正方形的边长为4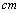 ,小正方形的边长为2
,小正方形的边长为2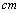 ,状态如图所示.大正方形固定不动,把小正方形以
,状态如图所示.大正方形固定不动,把小正方形以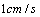 的速度向大正方形的内部沿直线平移,设平移的时间为
的速度向大正方形的内部沿直线平移,设平移的时间为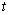 秒,两个正方形重叠部分的面积为
秒,两个正方形重叠部分的面积为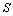
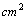 ,完成下列问题:
,完成下列问题:
1.用含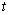 的式子表示
的式子表示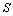 ,要求画出相应的图形,表明
,要求画出相应的图形,表明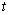 的范围;
的范围;
2.当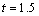 ,求重叠部分的面积
,求重叠部分的面积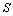 ;
;
3.当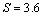
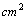 ,求
,求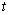 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com