
【题目】如图,已知△ABC:
(1)求作△ABC的内切圆⊙O,与边AB、BC、AC分别相切于点D、E、F;
(2)若AB=6,BC=8,AC=12,求AD、BE、CF的长度.

科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC于点F.
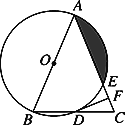
(1)判断DF与是⊙O的位置关系,并证明你的结论。
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
![]()
如果一个不等式中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式,求绝对值不等式|x|>3的解集.
小明同学的思路如下:
先根据绝对值的定义,求出|x|恰好是3时x的值,并在数轴上表示为点A,B,如图所示.观察数轴发现,以点A,B为分界点把数轴分为三部分:
点A左边的点表示的数的绝对值大于3;
点A,B之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论绝对值不等式|x|>3的解集为:x<-3或x>3.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①|x|>1的解集是 .
②|x|<2.5的解集是 .
(2)求绝对值不等式2|x-3|+5>13的解集.
(3)直接写出不等式x2>4的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程 x2-6x+m+4=0有两个实数根 x1,x2.
(1)求m的取值范围;
(2)若 x1,x2满足x2-2x1=-3 ,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两个可以自由转动的转盘,每个转盘分成三个相同的扇形,涂色情况如图所示,指针的位置固定,同时转动两个转盘,回答以下问题:

圆1 圆2
圆2 圆1 | |||
(1)补全表格:圆1的所有可能结果有 种,分别是 ;
圆2的所有可能结果有 种,分别是 .
(2)写出:转盘停止后指针指向同种颜色区域的概率和至少有一指针指向红色区域的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生的身高情况,王老师随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生人数相同,利用所得数据绘制如下统计图表:
组别 | 身高 |
|
|
|
|
|
|
|
|
|
|
身高情况分组表
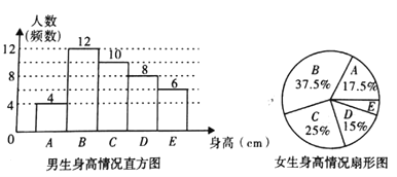
根据图表提供的信息,回答下列问题:
(1)样本中,女生身高在![]() 组的人数有_________人;
组的人数有_________人;
(2)在上面的扇形统计图中,表示![]() 组的扇形的圆心角是_________°;
组的扇形的圆心角是_________°;
(3)已知该校共有男生800人,女生760人,请估计该校身高在![]() 之间的学生约有多少人?
之间的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学1000名学生参加了“环保知识竞赛”,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x<90 | b | c |
合计 | ■ | 1 |
(1)写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
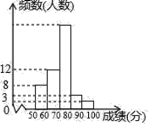
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠1+∠2=180°,∠B=∠D,CD平分∠ACF.
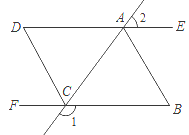
(1)DE与BF平行吗?请说明理由.
(2)AB与CD位置关系如何?为什么?
(3)AB平分∠CAE吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH=![]() BC,③BF=2OD,④∠CHF=45°.正确结论的个数为( )
BC,③BF=2OD,④∠CHF=45°.正确结论的个数为( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com