
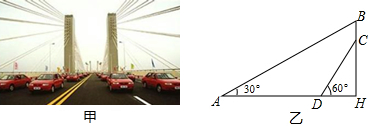
分析 设DH=x米,由三角函数得出=$\sqrt{3}$x,得出BH=BC+CH=2+$\sqrt{3}$x,求出AH=$\sqrt{3}$BH=2$\sqrt{3}$+3x,由AH=AD+DH得出方程,解方程求出x,即可得出结果.
解答 解:设DH=x米,
∵∠CDH=60°,∠H=90°,
∴CH=DH•tan60°=$\sqrt{3}$x,
∴BH=BC+CH=2+$\sqrt{3}$x,
∵∠A=30°,
∴AH=$\sqrt{3}$BH=2$\sqrt{3}$+3x,
∵AH=AD+DH,
∴2$\sqrt{3}$+3x=20+x,
解得:x=10-$\sqrt{3}$,
∴BH=2+$\sqrt{3}$(10-$\sqrt{3}$)=10$\sqrt{3}$-1≈16.3(米).
答:立柱BH的长约为16.3米.
点评 本题考查了解直角三角形的应用;由三角函数求出CH和AH是解决问题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:选择题

| A. | 120° | B. | 135° | C. | 150° | D. | 165° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO.下列结论:
如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO.下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com