练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，菱形ABCD的对角线AC，BD相交于点O，过点D作DE∥AC且DE=OC，连接CE，OE．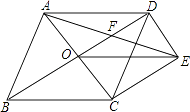
    （1）求证：OE=CD；
    （2）若菱形ABCD的边长为4，∠ABC=60°，求AE的长．

    【答案】
    （1）证明：在菱形ABCD中，OC= AC．

    ∴DE=OC．

    ∵DE∥AC，

    ∴四边形OCED是平行四边形．

    ∵AC⊥BD，

    ∴平行四边形OCED是矩形．

    ∴OE=CD．


    （2）解：在菱形ABCD中，∠ABC=60°，

    ∴AC=AB=4，

    ∴在矩形OCED中，

    CE=OD= = =2 ．

    在Rt△ACE中，

    AE= =2 ．


    【解析】（1）先求出四边形OCED是平行四边形，再根据菱形的对角线互相垂直求出∠COD=90°，证明OCED是矩形，可得OE=CD即可；（2）根据菱形的性质得出AC=AB，再根据勾股定理得出AE的长度即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

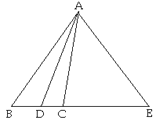
    【题目】如图，AD平分∠BAC，∠EAD＝∠EDA.

    （1）∠EAC与∠B相等吗？为什么？

    （2）若∠B＝50°,∠CAD︰∠E＝1︰3，求∠E的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在⊙O中，AB是弦，半径OC⊥AB，垂足为点D，要使四边形OACB为菱形，还需要添加一个条件，这个条件可以是（ ）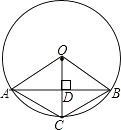
    A.AD=BD
    B.OD=CD
    C.∠CAD=∠CBD
    D.∠OCA=∠OCB

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：
    （1）2x2﹣4x﹣3=0（配方法）
    （2）x（x+2）=2+x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF． 求证：四边形BCFE是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

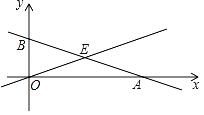
    【题目】如图，函数y=﹣x+2的图象与x轴、y轴分别交于点A、B，与函数y=kx（k为常数）的图象交于点E，以BE、OE为邻边的平行四边形是菱形．

    （1）求k；

    （2）过点B作y轴的垂线，交函数y=kx的图象于点C，四边形OACB是矩形吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合题。
    （1）解方程：x2=2x．
    （2）如图，Rt△ABC中，∠BAC=90°，AB=5，AC=12，将△ABC向右平移至△A′B′C′的位置，使得四边形ABB′A′为菱形，求B′C的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】.如图 1，AB∥CD，直线 EF 交 AB 于点 E，交 CD 于点 F，点 G 在 CD 上，点 P在直线 EF 左侧，且在直线 AB 和 CD 之间，连接 PE，PG.

    (1) 求证： ∠EPG=∠AEP＋∠PGC；

    (2) 连接 EG，若 EG 平分∠PEF，∠AEP+ ∠ PGE=110°，∠PGC=∠EFC，求∠AEP 的度数.

    (3) 如图 2，若 EF 平分∠PEB，∠PGC 的平分线所在的直线与 EF 相交于点 H，则∠EPG 与∠EHG之间的数量关系为　　　　　　.

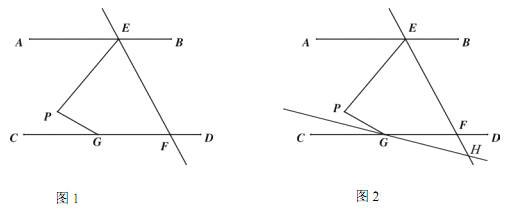
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中，P是BC上一点，且BP=3PC，Q是CD得中点．
    （1）证明△ADQ∽△QCP；
    （2）求证：AQ⊥QP．

    查看答案和解析>>

    同步练习册答案