
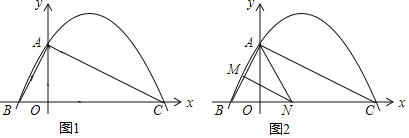
【题目】如图1,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;
(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)△ABC是直角三角形.理由见解析;(3)点N的坐标分别为(﹣8,0)、(8﹣4
x+4;(2)△ABC是直角三角形.理由见解析;(3)点N的坐标分别为(﹣8,0)、(8﹣4![]() ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4![]() ,0).(4)当△AMN面积最大时,N点坐标为(3,0).
,0).(4)当△AMN面积最大时,N点坐标为(3,0).
【解析】
(1)由点A、C的坐标利用待定系数法即可求出二次函数的解析式;(2)令二次函数解析式中y=0,求出点B的坐标,再由两点间的距离公式求出线段AB、AC、BC的长度,由三者满足AB2+AC2=BC2即可得出△ABC为直角三角形;(3)分别以A、C两点为圆心,AC长为半径画弧,与x轴交于三个点,由AC的垂直平分线与x轴交于一点,即可求得点N的坐标;(4)设点N的坐标为(n,0)(-2<n<8),通过分割图形法求面积,再根据相似三角形面积间的关系以及三角形的面积公式即可得出S△AMN关于n的二次函数关系式,根据二次函数的性质即可解决最值问题.
(1)∵二次函数y=ax2+![]() x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
∴![]() ,
,
解得![]() .
.
∴抛物线表达式:y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)△ABC是直角三角形.
令y=0,则﹣![]() x2+
x2+![]() x+4=0,
x+4=0,
解得x1=8,x2=﹣2,
∴点B的坐标为(﹣2,0),
由已知可得,
在Rt△ABO中AB2=BO2+AO2=22+42=20,
在Rt△AOC中AC2=AO2+CO2=42+82=80,
又∵BC=OB+OC=2+8=10,
∴在△ABC中AB2+AC2=20+80=102=BC2
∴△ABC是直角三角形.
(3)∵A(0,4),C(8,0),
∴AC=![]() =4
=4![]() ,
,
①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),
②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(8﹣4![]() ,0)或(8+4
,0)或(8+4![]() ,0)
,0)
③作AC的垂直平分线,交x轴于N,此时N的坐标为(3,0),
综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4![]() ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4![]() ,0).
,0).
(4)如图
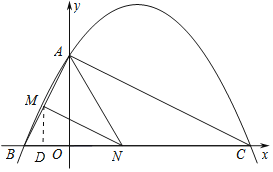 ,
,
设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,
∴MD∥OA,
∴△BMD∽△BAO,
∴![]() =
=![]() ,
,
∵MN∥AC
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵OA=4,BC=10,BN=n+2
∴MD=![]() (n+2),
(n+2),
∵S△AMN=S△ABN﹣S△BMN
=![]() BNOA﹣
BNOA﹣![]() BNMD
BNMD
=![]() (n+2)×4﹣
(n+2)×4﹣![]() ×
×![]() (n+2)2
(n+2)2
=﹣![]() (n﹣3)2+5,
(n﹣3)2+5,
当n=3时,△AMN面积最大是5,
∴N点坐标为(3,0).
∴当△AMN面积最大时,N点坐标为(3,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战
士们离营地的距离![]() 与时间
与时间![]() 之间函数关系的是( )
之间函数关系的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
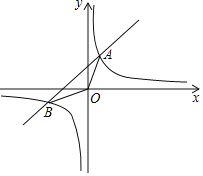
【题目】如图,已知一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w).
(m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w).
(1)求一次函数与反比例函数的解析式;
(2)在x轴的正半轴上找一点C,使△AOC的面积等于△ABO的面积,并求出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一根长为![]() 的铁丝剪成两段,并把每一段铁丝围成一个正方形.若设围成的一个正方形的边长为
的铁丝剪成两段,并把每一段铁丝围成一个正方形.若设围成的一个正方形的边长为![]() .
.
(1)要使这两个正方形的面积的和等于![]() ,则剪出的两段铁丝长分别是多少?
,则剪出的两段铁丝长分别是多少?
(2)剪出的两段铁丝长分别是多少![]() 时,这两个正方形的面积和最小?最小值是多少?
时,这两个正方形的面积和最小?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() ,抛物线过
,抛物线过![]() ,
,![]() 两点,点
两点,点![]() 是线段
是线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() .
.

(1)若抛物线的顶点![]() 的坐标为
的坐标为![]() ,其对称轴交
,其对称轴交![]() 于点
于点![]() ,
,
①求抛物线的解析式;
②是否存在点![]() ,使四边形
,使四边形![]() 为菱形?并说明理由;
为菱形?并说明理由;
(2)当点![]() 的横坐标为1时,是否存在这样的抛物线,使得以
的横坐标为1时,是否存在这样的抛物线,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出满足条件的抛物线的解析式:若不存在,请说明理由.
相似?若存在,求出满足条件的抛物线的解析式:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
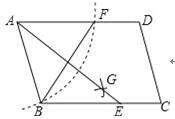
【题目】如图,在ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为( )
A. ![]() B. 2
B. 2![]() C. 3
C. 3![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有5个分别标有数字1,2,3,4,5的小球,它们的形状、大小、质地等完全相同.雄威同学先从盒子里随机取出第一个小球,记下数字为x;不放回盒子,再由丽贤同学随机取出第二个小球,记下数字为y.
(1)请用树状图或列表法表示出坐标(x,y)的所有可能出现的结果;
(2)求雄威同学、丽贤同学各取一个小球所确定的点(x,y)落在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某蛋糕店出售网红“奶昔包”,成本为30元/件,每天销售y(件)与销售单价x(元)之间存在一次函数关系,当以40元每件出售时,每天可以卖300件,当以55元每件出售时,每天可以卖150件.
(1)求y与x之间的函数关系式;
(2)如果规定每天“奶昔包”的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该蛋糕店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试直接写出该“奶昔包”销售单价的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com