
分析 根据分式的分子分母都乘以(或除以)同一个不为零整式,分式的值不变,可得答案.
解答 解:$\frac{{m}^{2012}+2{m}^{2013}+{m}^{2014}}{{m}^{2013}-{m}^{2015}}$,
=$\frac{{m}^{2012}(1+2m+{m}^{2})}{{m}^{2013}(1-{m}^{2})}$,
=$\frac{(m+1)^{2}}{m(1+m)(1-m)}$,
=$\frac{m+1}{m(1-m)}$,
=$\frac{1+m}{m-{m}^{2}}$,
∵m≠0,且|m|≠1,
∴分式$\frac{1+m}{m-{m}^{2}}$的分子和分母同时乘以m2012(m+1)后,得到$\frac{{m}^{2012}+2{m}^{2013}+{m}^{2014}}{{m}^{2013}-{m}^{2015}}$,
∴这个整式是m2012(m+1),
即m2013+m2012.
点评 本题考查了分式的基本性质和分解因式,熟练掌握分解因式是本题的关键,注意分母不能为0;利用分式的基本性质乘除时,要保证同乘(或除以)一个不等于0的整式,分式的值不变.


科目:初中数学 来源: 题型:解答题
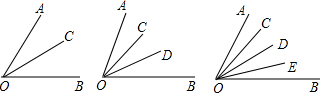
| ∠AOB内射线的条数 | 1 | 2 | 3 | 4 |
| 角的总个数 | 3 | 6 | 10 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com