
 14、相传古印度一座梵塔圣殿中,铸有一片巨大的黄铜板,之上树立了三米高的宝石柱,其中一根宝石柱上插有中心有孔的64枚大小两两相异的一寸厚的金盘,小盘压着较大的盘子,如图,把这些金盘全部一个一个地从1柱移到3柱上去,移动过程不许以大盘压小盘,不得把盘子放到柱子之外.移动之日,喜马拉雅山将变成一座金山.
14、相传古印度一座梵塔圣殿中,铸有一片巨大的黄铜板,之上树立了三米高的宝石柱,其中一根宝石柱上插有中心有孔的64枚大小两两相异的一寸厚的金盘,小盘压着较大的盘子,如图,把这些金盘全部一个一个地从1柱移到3柱上去,移动过程不许以大盘压小盘,不得把盘子放到柱子之外.移动之日,喜马拉雅山将变成一座金山.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源:2011年初中毕业升学考试(山东淄博卷)数学 题型:选择题
相传古印度一座梵塔圣殿中,铸有一片巨大的黄铜板,之上树立了三米高的宝石柱,其中一根宝石柱上插有中心有孔的64枚大小两两相异的一寸厚的金盘,小盘压着较大的盘子,如图,把这些金盘全部一个一个地从1柱移到3柱上去,移动过程不许以大盘压小盘,不得把盘子放到柱子之外。移动之日,喜马拉雅山将变成一座金山。
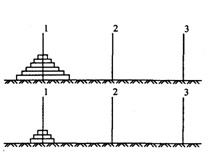
设h(n) 是把n个盘子从1柱移到3柱过程中移动盘子知最少次数
n=1时,h(1)=1
 n=2时,小盘 2柱,大盘 3柱,小柱从2柱 3柱,完成。即h(2)=3
n=2时,小盘 2柱,大盘 3柱,小柱从2柱 3柱,完成。即h(2)=3

 n=3时,小盘 3柱,中盘 2柱,小柱从3柱 2柱。 [即用h(2)
n=3时,小盘 3柱,中盘 2柱,小柱从3柱 2柱。 [即用h(2)
方法把中、小两盘移到2柱,大盘3柱;再用h(2)种方法把中、小两盘从2柱3柱,完成
我们没有时间去移64个盘子,但你可由以上移动过程的规律,计算n=6时, h(6)=
A.11 B.31 C.63 D.127
查看答案和解析>>
科目:初中数学 来源:2012年新思源教育学院中考数学模拟试卷(解析版) 题型:选择题
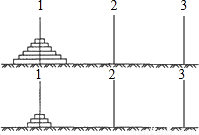
查看答案和解析>>
科目:初中数学 来源:2011年广西百色市中考数学试卷(解析版) 题型:选择题
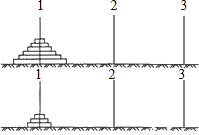
查看答案和解析>>
科目:初中数学 来源: 题型:
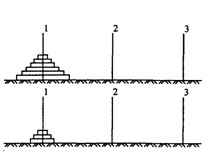


 n=2时,小盘 2柱,大盘 3柱,小柱从2柱 3柱,完成。即h(2)=3
n=2时,小盘 2柱,大盘 3柱,小柱从2柱 3柱,完成。即h(2)=3

 n=3时,小盘 3柱,中盘 2柱,小柱从3柱 2柱。 [即用h(2)
n=3时,小盘 3柱,中盘 2柱,小柱从3柱 2柱。 [即用h(2)| A.11 | B.31 | C.63 | D.127 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com