
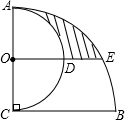
 如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )| A. | $\frac{5}{3}π-2\sqrt{3}$ | B. | $\frac{5}{3}π-4$ | C. | $3π-2\sqrt{3}$ | D. | 3π-4 |
分析 连接CE,由图可知S阴影=S扇形ACB-S扇形AOD-S扇形ECB-S△OCE.根据已知条件易求得OA=OC=OD=2,BC=CE=4.∠ECB=∠OEC=30°,所以由扇形面积公式、三角形面积公式进行解答即可.
解答 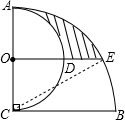 解:如图,连接CE.
解:如图,连接CE.
∵AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{AB}$,
∴∠ACB=90°,OA=OC=OD=2,BC=CE=4.
又∵OE∥BC,
∴∠AOE=∠COE=90°.
∴在直角△OEC中,OC=$\frac{1}{2}$CE,
∴∠OEC=30°,OE=2$\sqrt{3}$.
∴∠ECB=∠OEC=30°,
∴S阴影=S扇形ACB-S扇形AOD-S扇形ECB-S△OCE=$\frac{90π×{4}^{2}}{360}$-$\frac{90π×{2}^{2}}{360}$-$\frac{30π×{4}^{2}}{360}$-$\frac{1}{2}$×2×2$\sqrt{3}$=$\frac{5}{3}$π-2$\sqrt{3}$.
故选A.
点评 本题考查了扇形面积的计算.不规则图形的面积一定要注意分割成规则图形的面积进行计算.


科目:初中数学 来源: 题型:解答题
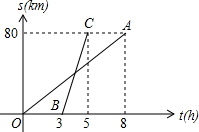 如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:
如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y2<y3<y1 | D. | y3>y2>y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
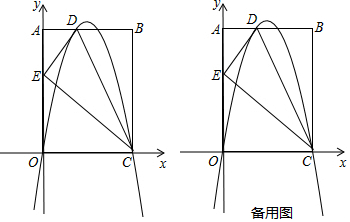
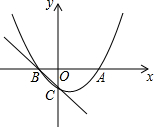 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与y轴相交于C,与x轴帕交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与y轴相交于C,与x轴帕交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,顶点为(-4,1)的抛物线交y轴于A点,交x轴于B、C两点(点B在C的右侧),已知A点坐标为(0,-3).
如图,在平面直角坐标系中,顶点为(-4,1)的抛物线交y轴于A点,交x轴于B、C两点(点B在C的右侧),已知A点坐标为(0,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
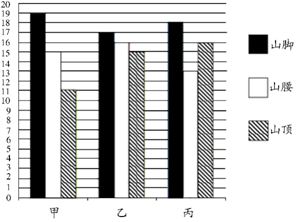 甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断:
甲,乙,丙三种作物,分别在山脚,山腰和山顶三个试验田进行试验,每个试验田播种二十粒种子,农业专家将每个试验田成活的种子个数统计如条形统计图,如图所示,下面有四个推断:| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
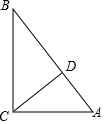 已知关于x的方程x2-2(a+b)x+c2+2ab=0有两个相等的实数根,其中a、b、c为△ABC的三边长.
已知关于x的方程x2-2(a+b)x+c2+2ab=0有两个相等的实数根,其中a、b、c为△ABC的三边长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com