
根据题意,解答问题:

(1)如图1,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长.
(2)如图2,类比(1)的解题过程,请你通过构造直角三角形的方法,求出点M(3,4)与点N(﹣2,﹣1)之间的距离.
(3)在(2)的基础上,若有一点D在x轴上运动,当满足DM=DN时,请求出此时点D的坐标.
考点:
一次函数综合题..
分析:
(1)由一次函数解析式求得点A、B的坐标,则易求直角△AOB的两直角边OB、OA的长度,所以在该直角三角形中利用勾股定理即可求线段AB的长度;
(2)如图2,过M点作x轴的垂线MF,过N作y轴的垂线NE,MF和NE交于点C,构造直角△MNC,则在该直角三角形中利用勾股定理来求求点M与点N间的距离;
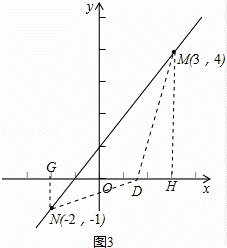
(3)如图3,设点D坐标为(m,0),连结ND,MD,过N作NG垂直x轴于G,过M作MH垂直x轴于H.在直角△DGN和直角△MDH中,利用勾股定理得到关于m的方程12+(m+2)=42+(3﹣m)2
通过解方程即可求得m的值,则易求点D的坐标.
解答:
解:(1)令x=0,得y=4,即A(0,4).
令y=0,得x=﹣2,即B(﹣2,0).
在Rt△AOB中,根据勾股定理有:
![]() ;
;
(2)如图2,过M点作x轴的垂线MF,过N作y轴的垂线NE,MF和NE交于点C.
根据题意:MC=4﹣(﹣1)=5,NC=3﹣(﹣2)=5.
则在Rt△MCN中,根据勾股定理有:
![]() ;
;
(3)如图3,设点D坐标为(m,0),连结ND,MD,过N作NG垂直x轴于G,过M作MH垂直x轴于H.
则GD=|m﹣(﹣2)|,GN=1,DN2=GN2+GD2=12+(m+2)2
MH=4,DH=|3﹣m|,DM2=MH2+DH2=42+(3﹣m)2
∵DM=DN,
∴DM2=DN2
即12+(m+2)=42+(3﹣m)2
整理得:10m=20 得m=2
∴点D的坐标为(2,0).
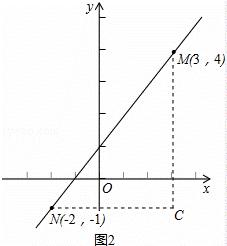
点评:
本题考查了勾股定理、一次函数图象上点的坐标特征.注意:突破此题的难点的方法是辅助线的作法.


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
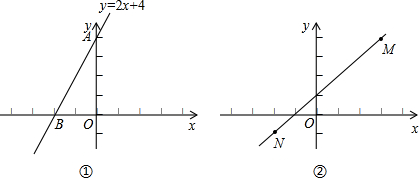
查看答案和解析>>
科目:初中数学 来源:2011年内蒙古呼伦贝尔市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com