
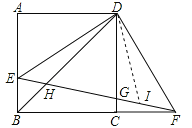
【题目】如图,正方形ABCD中,E为AB边上一点,过点D作DF⊥DE,与BC延长线交于点F.连接EF,与CD边交于点G,与对角线BD交于点H.
(1)若BF=BD=![]() ,求BE的长;
,求BE的长;
(2)若∠ADE=2∠BFE,求证:FH=HE+HD.

【答案】(1)BE=2-![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】分析:(1)由四边形ABCD正方形,BF=BD=![]() ,由勾股定理即可求得BC的长,又由DF⊥DE,易证得△ADE≌△CDF,即可求得BE的长;
,由勾股定理即可求得BC的长,又由DF⊥DE,易证得△ADE≌△CDF,即可求得BE的长;
(2)首先在FE上截取一段FI,使得FI=EH,由△ADE≌△CDF,易证得△DEH≌△DFI,即可得DH=DI,又由∠ADE=2∠BFE,易证得△DHI为等边三角形,即可得DH=HI,继而可得FH=HE+HD.
详解:(1)解:∵四边形ABCD正方形,∴∠BCD=90°,BC=CD,∴Rt△BCD中,BC2+CD2=BD2,即BC2=(![]() )2﹣(BC)2,∴BC=AB=1.∵DF⊥DE,∴∠ADE+∠EDC=90°=∠EDC+∠CDF,∴∠ADE=∠CDF.在△ADE和△CDF中,∵
)2﹣(BC)2,∴BC=AB=1.∵DF⊥DE,∴∠ADE+∠EDC=90°=∠EDC+∠CDF,∴∠ADE=∠CDF.在△ADE和△CDF中,∵ ,∴△ADE≌△CDF(ASA),∴AE=CF=BF﹣BC=
,∴△ADE≌△CDF(ASA),∴AE=CF=BF﹣BC=![]() ﹣1,∴BE=AB﹣AE=1﹣(
﹣1,∴BE=AB﹣AE=1﹣(![]() ﹣1)=2﹣
﹣1)=2﹣![]() ;
;
(2)证明:在FE上截取一段FI,使得FI=EH.∵△ADE≌△CDF,∴DE=DF,∴△DEF为等腰直角三角形,∴∠DEF=∠DFE=45°=∠DBC.∵∠DHE=∠BHF,∴∠EDH=∠BFH(三角形的内角和定理).在△DEH和△DFI中,∵ ,∴△DEH≌△DFI(SAS),∴DH=DI.又∵∠HDE=∠BFE,∠ADE=2∠BFE,∴∠HDE=∠BFE=
,∴△DEH≌△DFI(SAS),∴DH=DI.又∵∠HDE=∠BFE,∠ADE=2∠BFE,∴∠HDE=∠BFE=![]() ∠ADE.∵∠HDE+∠ADE=45°,∴∠HDE=15°,∴∠DHI=∠DEH+∠HDE=60°,即△DHI为等边三角形,∴DH=HI,∴FH=FI+HI=HE+HD.
∠ADE.∵∠HDE+∠ADE=45°,∴∠HDE=15°,∴∠DHI=∠DEH+∠HDE=60°,即△DHI为等边三角形,∴DH=HI,∴FH=FI+HI=HE+HD.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF;②∠AEF=45°;③S四边形EFHG=S△DEF+S△AGH;④△AEF≌△CDE

其中正确的结论有______ (填正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B′C′的位似比;
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A′B′C′关于点O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x+2)2+3(a<0)的图象如图所示,则以下结论:①当x>﹣2时,y随x的增大而增大;②不论a为任何负数,该二次函数的最大值总是3;③当a=﹣1时,抛物线必过原点;④该抛物线和x轴总有两个公共点.其中正确结论是( )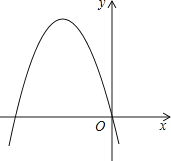
A.①②
B.②③
C.②④
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学小组的10位同学站成一列做报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己顺序的倒数的2倍加1,第1位同学报 ![]() ,第2位同学报
,第2位同学报 ![]() ,第3位同学报
,第3位同学报 ![]() ,…这样得到10个数的积为 .
,…这样得到10个数的积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,BC=AC=5,AB=8,CD为AB边上的高,如图1,A在原点处,点B在y轴正半轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒1个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面上滑动.如图2,设运动时间表为t秒,当B到达原点时停止运动.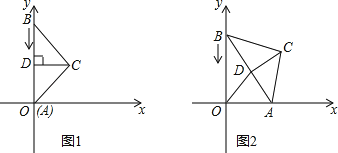
(1)当t=0时,求点C的坐标;
(2)当t=4时,求OD的长及∠BAO的大小;
(3)求从t=0到t=4这一时段点D运动路线的长;
(4)当以点C为圆心,CA为半径的圆与坐标轴相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大众汽车经销商在销售某款汽车时,以高出进价20%标价.已知按标价的九折销售这款汽车9辆与将标价直降0.2万元销售4辆获利相同.
(1)求该款汽车的进价和标价分别是多少万元?
(2)若该款汽车的进价不变,按(1)中所求的标价出售,该店平均每月可售出这款汽车20辆;若每辆汽车每降价0.1万元,则每月可多售出2辆.求该款汽车降价多少万元出售每月获利最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com