练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．下列说法中正确的个数有（　　）
    ①有一个角为60°的等腰三角形是等边三角形；
    ②三边长为$\sqrt{14}$，$\sqrt{5}$，3的三角形为直角三角形；
    ③等腰三角形的两条边长为2，4，则等腰三角形的周长为10或8；
    ④一边上的中线等于这边长的一半的三角形是等腰直角三角形．
    A．1个B．2个C．3个D．4个

    分析 根据等边三角形的判定可得①正确；根据勾股定理逆定理可判定出②正确；根据三角形的三边关系可得2只能当底，不能当腰，因此周长为10，故③错误；一边上的中线等于这边长的一半的三角形是直角三角形，故④错误．

    解答 解：①有一个角为60°的等腰三角形是等边三角形，说法正确；
    ②三边长为$\sqrt{14}$，$\sqrt{5}$，3的三角形为直角三角形，说法正确；
    ③等腰三角形的两条边长为2，4，则等腰三角形的周长为10或8，说法错误；
    ④一边上的中线等于这边长的一半的三角形是等腰直角三角形，说法错误．
    正确的说法有2个．
    故选：B．

    点评 此题主要考查了等边三角形的判定、勾股定理逆定理、直角三角形判定、以及等腰三角形，关键是掌握等边三角形的判定定理，三角形的三边关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

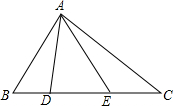    1．在△ABC中，AB=14，AE=12，BD=7，BC=28，且∠BAD=∠EAC．
    （1）EC的长？
    （2）△AED∽△BEA是否相似？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．请先观察下列算式，再填空：32-12=8×1，52-32=8×2，72-52=8×3，92-72=8×4，…，通过观察归纳，写出反映这种规律的一般结论：（2n+1）2-（2n-1）2=8n．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．阅读下列材料，解答下列问题：
    材料1．把一个多项式化成几个整式的积的形式，这种变形叫做因式分解，也叫分解因式．如果把整式的乘法看成一个变形过程，那么多项式的因式分解就是它的逆过程．
    公式法（平方差公式、完全平方公式）是因式分解的一种基本方法．如对于二次三项式a2+2ab+b2，可以逆用乘法公式将它分解成（a+b）2的形式，我们称a2+2ab+b2为完全平方式．但是对于一般的二次三项式，就不能直接应用完全平方了，我们可以在二次三项式中先加上一项，使其配成完全平方式，再减去这项，使整个式子的值不变，于是有：
    x2+2ax-3a2
    =x2+2ax+a2-a2-3a2
    =（x+a）2-（2a）2
    =（x+3a）（x-a）
    材料2．因式分解：（x+y）2+2（x+y）+1
    解：将“x+y”看成一个整体，令x+y=A，则
    原式=A2+2A+1=（A+1）2
    再将“A”还原，得：原式=（x+y+1）2．
    上述解题用到的是“整体思想”，整体思想是数学解题中常见的一种思想方法，请你解答下列问题：
    （1）根据材料1，把c2-6c+8分解因式；
    （2）结合材料1和材料2完成下面小题：
    ①分解因式：（a-b）2+2（a-b）+1；
    ②分解因式：（m+n）（m+n-4）+3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图是“明清影视城”的圆弧形门，这个圆弧形门所在的圆与水平地面是相切的，AB=CD=20cm，BD=200cm，且AB，CD与水平地面都是垂直的．则这个圆弧形门的最高点离地面的高度是520 cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．方程$\frac{5}{{x}^{2}+x}$+$\frac{3}{{x}^{2}-x}$=$\frac{6}{{x}^{2}-1}$的解为（　　）
    A．x=1B．x=-1C．x=$\frac{3}{5}$D．无解

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．阅读材料：若m2-2mn+2n2-2n+1=0，求m、n的值．
    解：∵m2-2mn+2n2-2n+1=0，∴（m2-2mn+n2）+（n2-2n+1）=0
    ∴（m-n）2+（n-1）2=0，∴（m-n）2=0，（n-1）2=0，∴n=1，m=1．
    根据你的观察，探究下面的问题：
    （1）已知x2+2xy+2y2+2y+1=0，求x、y的值；
    （2）已知a，b，c是△ABC的三边长，满足a2+b2=12a+8b-52，且△ABC是等腰三角形，求c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

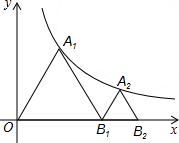    20．如图，点A1，A2依次在y=$\frac{4\sqrt{3}}{x}$（x＞0）的图象上，点B1，B2依次在x轴的正半轴上，若△A1OB1，△A2B1B2均为等边三角形，则点B2的坐标为（　　）
    A．（4，0）B．（4$\sqrt{2}$，0）C．（6，0）D．（6$\sqrt{2}$，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．学习了数据的收集、整理与表示之后，某小组同学对本校“自主选修活动课”比较感兴趣，他们以问卷的形式随机调查了40名学生的选课情况（每人只能选一项），并统计如下：
    科目篮球围棋剪纸舞台剧茶艺交谊舞其它课
    计数正正 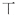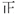正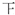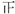正一正一
    （1）请选择一种统计图将上表中的结果表示出来；
    （2）该校共有500名学生，请估计选修篮球课的人数；并说明你估计的理由；
    （3）谈谈你对该校“自主选修活动课”的科目设置有哪些建议？

    查看答案和解析>>

    同步练习册答案