
 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.分析 (1)将原三角形的三顶点分别向左平移4个单位得到其对应点,顺次连接即可得;
(2)利用平移的性质得出AC与A1C1的关系;
(3)根据三角形高的定义可得;
(4)过点C作平行于AB的直线、再AB的另一侧作直线平行于AB且该直线到AB的距离等于CD,据此可得;
(5)延长BA交直线B1C1于点P,此时|PA-PB|=AB,最大.
解答 解:(1)如图所示,△A1B1C1即为所求;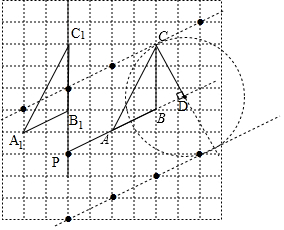
(2)AC与A1C1的关系是:平行且相等,
故答案为:平行且相等;
(3)如图,CD即为所求;
(4)如图,能使S△QAB=S△ABC的格点Q(异于点C)的个数有8个,
故答案为:8;
(5)如图,点P即为所求.
点评 本题主要考查作图-平移变换,熟练掌握平移的定义和性质及三角形三边之间的关系是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
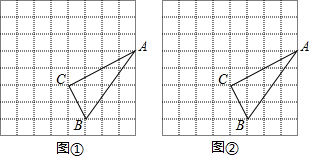 如图,小方格的边长为1,△ABC为格点三角形.
如图,小方格的边长为1,△ABC为格点三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{2}$ | $\frac{20}{3}$ | 5 | 4 | m | $\frac{20}{3}$ | $\frac{17}{2}$ | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com