
【题目】如图,PA,PB是⊙O的切线,A,B是切点,点C是劣弧AB上的一点,若∠P=40°,则∠ACB等于( )
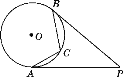
A. 80° B. 110° C. 120° D. 140°
【答案】B
【解析】
连接OA,OB,在优弧AB上任取一点D(不与A、B重合),连接BD,AD,如图所示,由PA与PB都为圆O的切线,利用切线的性质得到OA与AP垂直,OB与BP垂直,在四边形APBO中,根据四边形的内角和求出∠AOB的度数,再利用同弧所对的圆周角等于所对圆心角的一半求出∠ADB的度数,再根据圆内接四边形的对角互补即可求出∠ACB的度数.
连接OA,OB,在优弧AB上任取一点D(不与A、B重合),
连接BD,AD,如图所示:
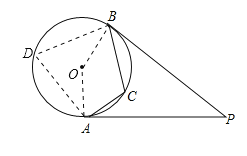
∵PA、PB是⊙O的切线,
∴OA⊥AP,OB⊥BP,
∴∠OAP=∠OBP=90°,又∠P=40°,
∴∠AOB=360°-(∠OAP+∠OBP+∠P)=140°,
∵圆周角∠ADB与圆心角∠AOB都对弧AB,
∴∠ADB=![]() ∠AOB=70°,
∠AOB=70°,
又四边形ACBD为圆内接四边形,
∴∠ADB+∠ACB=180°,
则∠ACB=110°.
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
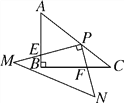
查看答案和解析>>
科目:初中数学 来源: 题型:
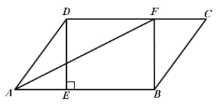
【题目】如图,在平行四边形 ABCD 中,过点 D 作 DE AB 于点 E ,点 F在边 CD 上, DF BE ,连接 AF , BF .
(1)求证:四边形 BFDE 是矩形;
(2)若 AF 平分 DAB , CF3,BF4 ,求 DF 长.
查看答案和解析>>
科目:初中数学 来源: 题型:
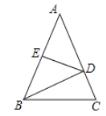
【题目】△ABC中,AB=AC,AB的垂直平分线DE交AB、AC于点E、D,若△ABC和△BCD的周长分别为21cm和13cm,求△ABC的各边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连结BE交AC于F,连结FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD②△FED与△DEB③△CFD与△ABG④△ADF与△CFB中相似的为( )

A. ①④B. ①②C. ②③④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
课外兴趣小组活动时,老师提出了如下问题:如图1,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.请根据小明的方法思考:

(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(初步运用)
如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
(灵活运用)
如图3,在△ABC中,∠A=90°,D为BC中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF,试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com