
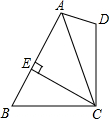
 已知,如图,在凸四边形ABCD中,AC平分∠BAD,过点C作CE⊥AB,E为垂足,BC=CD,求证:AE=$\frac{1}{2}$(AB+AD).
已知,如图,在凸四边形ABCD中,AC平分∠BAD,过点C作CE⊥AB,E为垂足,BC=CD,求证:AE=$\frac{1}{2}$(AB+AD). 分析 过C作CM⊥AD于M,证△MAC≌△EAC,推出AM=AE,证Rt△DMC≌Rt△BEC,推出BE=DM,求出AB+AD=AE+BE+AD=AE+DM+AD=2AM=2AE,即可得出答案.
解答 证明:过C作CM⊥AD于M,如图,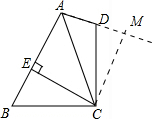
∵CE⊥AB,
∴∠M=∠CEB=90°,
∵∠ABC+∠ADC=180°,∠ADC+°,
∴∠B=∠MDC,
∵AC平分∠BAD,CM⊥AD,CE⊥AB,
∴CM=CE,∠MAC=∠EAC,
在△MAC和△EAC中,
$\left\{\begin{array}{l}{∠MAC=∠EAC}\\{∠M=∠AEC=90°}\\{AC=AC}\end{array}\right.$,
∴△MAC≌△EAC(AAS),
∴AM=AE,
∵∠M=∠BEC=90°,
∴在Rt△DMC和Rt△BEC中
$\left\{\begin{array}{l}{CD=BC}\\{CM=CE}\end{array}\right.$
∴Rt△DMC≌Rt△BEC(HL),
∴BE=DM,
∴AB+AD
=AE+BE+AD
=AE+DM+AD
=2AM
=2AE,
即AE=$\frac{1}{2}$(AB+AD).
点评 本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应边相等,对应角相等,题目比较好,难度适中.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:填空题
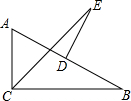 如图,在△ABC中,已知AC=5,BC=12,AB=13,D为边AB的中点,DE⊥AB且与∠ACB的平分线交于点E,则DE的长为$\frac{13}{2}$.
如图,在△ABC中,已知AC=5,BC=12,AB=13,D为边AB的中点,DE⊥AB且与∠ACB的平分线交于点E,则DE的长为$\frac{13}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某批汽车的抗撞击能力 | |
| B. | 鞋厂检测生产的鞋底能承受的弯折次数 | |
| C. | 了解全班学生的视力情况 | |
| D. | 检测吉林市某天的空气质量 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
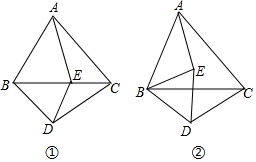
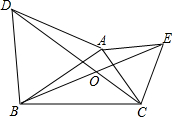 如图,以△ABC的边AB,AC为边长向外作等边△ABD和等边△ACE,连接BE,CD相交于点O.△ABC中,∠BAC=90°,∠ABC=30°,且BC=2,OB的长为$\frac{4\sqrt{7}}{7}$.
如图,以△ABC的边AB,AC为边长向外作等边△ABD和等边△ACE,连接BE,CD相交于点O.△ABC中,∠BAC=90°,∠ABC=30°,且BC=2,OB的长为$\frac{4\sqrt{7}}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
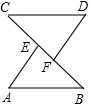 如图,已知EC=BF,AB∥CD,现有下列5个条件:①AE=DF;②∠B=∠C;③DF∥AE;④∠A=∠D;⑤AB=CD;从中选取一个条件,以保证△ABE≌△DCF,则可选择的有( )
如图,已知EC=BF,AB∥CD,现有下列5个条件:①AE=DF;②∠B=∠C;③DF∥AE;④∠A=∠D;⑤AB=CD;从中选取一个条件,以保证△ABE≌△DCF,则可选择的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com