
【题目】如图,在正方形![]() 中,以
中,以![]() 为边作等边
为边作等边![]() ,延长
,延长![]() ,
,![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 与
与![]() 相交于点
相交于点![]() ,给出下列结论:①
,给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的是__________.
,其中正确的是__________.
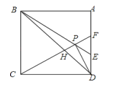
【答案】①②③④
【解析】
①正确.利用直角三角形30度角的性质即可解决问题;②正确,通过计算证明∠BPD=135°,即可判断; ③正确,根据两角相等两个三角形相似即可判断;④正确.利用相似三角形的性质即可证明.
∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ABC =∠ADC=∠BCD=90°,
∴∠ABE=∠DCF=90°-60°=30°,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴在![]() 中,∠A=90°,∠ABE=30°,
中,∠A=90°,∠ABE=30°,
∴![]() ,故①正确;
,故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=∠DPC=![]() 75°,
75°,
∴∠BPD=∠BPC+∠DPC =60°+75°=135°,故②正确;
∵∠ADC =90°,∠PDC=75°,
∴∠EDP=∠ADC -∠PDC =90°-75°=15°,
∵∠DBA=45°,∠ABE=30°,
∴∠EBD=∠DBA -∠ABE =45°-30°=15°,
∴∠EDP=∠EBD=15°,
∵∠DEP=∠BED,
∴△PDE∽△DBE,故③正确;
∵△PDE∽△DBE,
∴![]() ,
,
∴![]() ,故④正确;
,故④正确;
综上,①②③④都正确,
故答案为:①②③④.


科目:初中数学 来源: 题型:
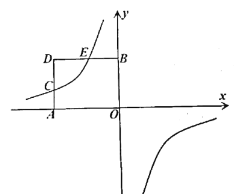
【题目】如图,在平面直角坐标系中,已知矩形![]() 的顶点
的顶点![]() ,过点
,过点![]() 的双曲线
的双曲线![]() 与矩形
与矩形![]() 的边
的边![]() 交于点
交于点![]() .
.
(1)求双曲线![]() 的解析式以及点
的解析式以及点![]() 的坐标;.
的坐标;.
(2)若点![]() 是抛物线
是抛物线![]() 的顶点;
的顶点;
①当双曲线![]() 过点
过点![]() 时,求顶点
时,求顶点![]() 的坐标;
的坐标;
②直接写出当抛物线![]() 过点
过点![]() 时,该抛物线与矩形
时,该抛物线与矩形![]() 公共点的个数以及此时
公共点的个数以及此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
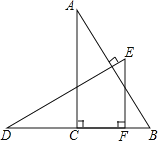
【题目】如图,△ABC和△DEF都是直角三角形,∠ACB=∠DFE=90°,AB=DE,顶点F在BC上,边DF经过点C,点A,E在BC同侧,DE⊥AB.
(1)求证:△ABC≌△DEF;
(2)若AC=11,EF=6,CF=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动(不与点A,B重合);同时点Q从点C出发沿CD以2cm/s的速度向点D移动(不与点C、D重合),经过几秒,△PDQ为直角三角形?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
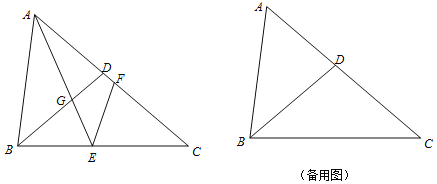
【题目】如图,已知△ABC中,AB=8,BC=10,AC=12,D是AC边上一点,且AB2=ADAC,连接BD,点E、F分别是BC、AC上两点(点E不与B、C重合),∠AEF=∠C,AE与BD相交于点G.
(1)求BD的长;
(2)求证△BGE∽△CEF;
(3)连接FG,当△GEF是等腰三角形时,直接写出BE的所有可能的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
![]() 求出每天的销售利润
求出每天的销售利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
![]() 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?
如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?![]() 每天的总成本
每天的总成本![]() 每件的成本
每件的成本![]() 每天的销售量
每天的销售量![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
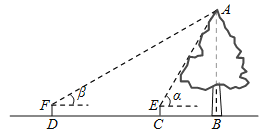
【题目】如图,AB是一棵古树,某校初四(1)班数学兴趣小组的同学想利用所学知识测出这棵古树的高,过程如下:在古树同侧的水平地面上,分别选取了C、D两点(C、D两点与古树在同一直线上),用测角仪在C处测得古树顶端A的仰角α=60°,在D处测得古树顶端A的仰角β=30°,又测得C、D两点相距14米.已知测角仪高为1.5米,请你根据他们所测得的数据求出古树AB的高.(精确到0.1米,![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com