
����Ŀ����ͼ��CD�Ǿ�����BCA�Ķ���C��һ��ֱ�ߣ�CA��CB��E��F��ֱ��CD�ϵ����㣬�ҡ�BEC����CFA����.
(1)��ֱ��CD������BCA���ڲ�����E��F������CD�ϣ����������������⣺
����ͼ(a)������BCA��90�㣬����90������BE________CF��EF________|BE��AF|(����>����<����������)��
����ͼ(b)����0�㣼��BCA��180����������һ�����������BCA��ϵ������________��ʹ���е�����������Ȼ��������֤���������۳�����
(2)��ͼ(c)����ֱ��CD������BCA���ⲿ����BCA��������д��EF��BE��AF�����߶�������ϵ�ĺ�������(��Ҫ��֤��)��

���𰸡�(1)����������������������ǣ�������BCA��180��.֤����������(2)EF��BE��AF.
��������
(1)�������BEC=��AFC=90�㣬��CBE=��ACF������AAS֤��BCE�ա�CAF���Ƴ�BE=CF��CE=AF���ɣ��������BEC=��AFC����CBE=��ACF������AAS֤��BCE�ա�CAF���Ƴ�BE=CF��CE=AF����
(2)�����BEC=��AFC����CBE=��ACF������AAS֤��BCE�ա�CAF���Ƴ�BE=CF��CE=AF����.
�⣺(1)����ͼ��E����F�����࣬
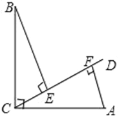
��BE��CD��AF��CD����ACB=90�㣬
���BEC=��AFC=90�㣬
���BCE����ACF=90�㣬��CBE+��BCE=90�㣬
���CBE=��ACF��
�ڡ�BCE�͡�CAF��
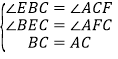 ��
��
���BCE�ա�CAF(AAS)��
��BE=CF��CE=AF��
��EF=CF��CE=BE��AF��
��E��F���Ҳ�ʱ��ͬ����֤EF=AF��BE��
��EF=|BE��AF|��
�ڡϦ�����ACB=180��ʱ����������������Ȼ������
֤�����ߡ�BEC=��CFA=��a���Ϧ�����ACB=180�㣬
���CBE=��ACF��
�ڡ�BCE�͡�CAF��
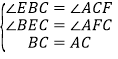 ��
��
���BCE�ա�CAF��AAS����
��BE=CF��CE=AF��
��EF=CF��CE=BE��AF��
��E��F���Ҳ�ʱ��ͬ����֤EF=AF��BE��
��EF=|BE��AF|��
(2)EF=BE��AF
�����ǣ��ߡ�BEC=��CFA=��a����a=��BCA��
�֡ߡ�EBC+��BCE+��BEC=180�㣬��BCE+��ACF+��ACB=180�㣬
���EBC+��BCE=��BCE+��ACF��
���EBC=��ACF��
�ڡ�BEC�͡�CFA��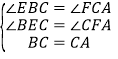 ��
��
���BEC�ա�CFA(AAS)��
��AF=CE��BE=CF��
��EF=CE��CF��
��EF=BE��AF.


 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߳�Ϊm�����������Ϊ12�������й���m��˵���У�������ǣ� ��
��m������������m�Ƿ���m2 -12=0�Ľ⣻��m���㲻��ʽ��![]() ����m��12������ƽ������
����m��12������ƽ������
A. �٢� B. �٢� C. �� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
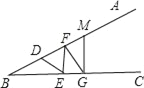
����Ŀ����֪����ͼ��BD=DE=EF=FG��
��1������ABC=20�㣬��ABC�ڷ�������BD=DE=EF=FG�����ߣ���DE��EF��FG�����м���������ABC=10���أ���һ�ԣ����������ɣ�
��2������ABC=m�㣨0��m��90���������ҳ�һ����������n��m֮��Ĺ�ϵ�����У����ҳ��������ޣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��CE��AB�ڵ�E��BD��AC�ڵ�D��BD��CE���ڵ�O����AOƽ�֡�BAC����ͼ�е�ȫ�������ι���________�ԣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A=2x2+ax��5y+b��B=bx2��![]() x��
x��![]() y��3��
y��3��
��1����3A����4A��2B����ֵ��
��2����xȡ������ֵ��A��2B��ֵ��һ����ֵʱ����a+![]() A������2b+
A������2b+![]() B����ֵ��
B����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=130��������OC����AOB�ڲ�����һ�����ߣ�OD��OE�ֱ�����AOC����BOC�Ľ�ƽ���ߣ�����������ȷ���ǣ�������
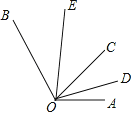
A. ��DOE�Ķ�������ȷ�� B. ��AOD=![]() ��EOC
��EOC
C. ��AOD+��BOE=65�� D. ��BOE=2��COD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
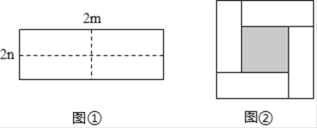
����Ŀ��ͼ����һ����Ϊ2m����Ϊ2n�ij�����ֽƬ����������ֽƬ��ͼ���������ĸ���״�ʹ�С��ȫ��ͬ��С�����Σ�Ȼ��ƴ��ͼ����ʾ��һ���������Σ�
��1�������ֲ�ͬ�ķ�����ʾͼ����С�����Σ���Ӱ���֣��������
����һ��SС������=�� ����
��������S������=�� ����
��2����m+n��2����m��n��2��mn����������ʽ֮��ĵ�����ϵΪ�� ��
��3��Ӧ�ã�2���з��ֵĹ�ϵʽ������⣺��x+y=9��xy=14����x��y��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
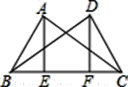
����Ŀ����ͼ��ʾ����ABC����DCB�й�����BC����AB=DC����AE��BC��DF��BC������ֱ�ΪE��F��AE=DF����ô��֤AC=BDʱ����Ҫ֤��������ȫ�ȵ���Rt��ABE��Rt��DCF����AEC��DFB��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����Լ�������ƽ������һ�����ԣ�����������Էֳ����ĸ�������������ߴ���ͼ��ʾ��ͼ�г��ȵ�λ��������С�żƻ������ĸ������ϰ�ͼ����ʾ�ֱ���ֲ�ݱ����� 1 �š�2 �š�3 �š�4 �ţ�
��1����ʽ�ӱ�ʾ������Ե��������
��2����֪��ֲ�ݱ����� 1 �š�2 �š�3 �š�4 �ŵijɱ��ֱ���ÿƽ���� 4 Ԫ��6 Ԫ��8 Ԫ��10 Ԫ��
����ʽ�ӱ�ʾС���������������ֲ�ݱ����ܵ��ܳɱ���
�ڵ� a=9 ʱ����С���������������ֲ�ݱ����ܵ��ܳɱ���

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com