
分析 设人数有x人,鸡的价钱是y钱,根据每人出8钱,多余3钱得出等量关系一:鸡的价钱=8×买鸡人数-3;根据每人出7钱,还缺4钱得出等量关系二:鸡的价钱=7×买鸡人数+4,依此两个等量关系列出方程组即可.
解答 解:设人数有x人,鸡的价钱是y钱,
由题意得 $\left\{\begin{array}{l}{y=8x-3}\\{y=7x+4}\end{array}\right.$.
故答案为$\left\{\begin{array}{l}{y=8x-3}\\{y=7x+4}\end{array}\right.$.
点评 此题考查了由实际问题抽象出二元一次方程组,根据鸡价得到等量关系是解决本题的关键.


科目:初中数学 来源: 题型:选择题
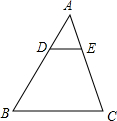 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{AC}$=$\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
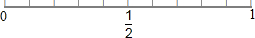 将下列事件发生的概率填在图中:(只填各事件的序号)
将下列事件发生的概率填在图中:(只填各事件的序号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
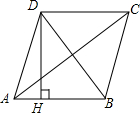 如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )
如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( )| A. | $\frac{24}{5}$ | B. | $\frac{12}{5}$ | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
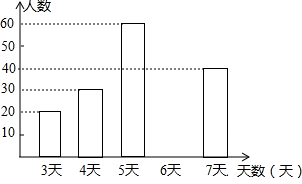
| 天数 | 频数 | 频率 |
| 3 | 20 | 0.10 |
| 4 | 30 | 0.15 |
| 5 | 60 | 0.30 |
| 6 | a | 0.25 |
| 7 | 40 | 0.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A(m,4),B(-4,n)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.
如图,点A(m,4),B(-4,n)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
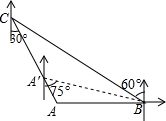 如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.
如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com