
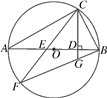
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】一块木板如图所示,已知AB=4,BC=3,DC=12,AD=13,∠B=90°,木板的面积为( )

A. 60 B. 30 C. 24 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC上的一点,连接AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
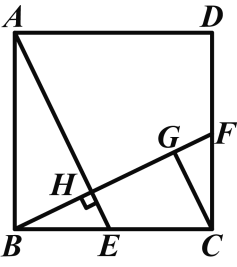
求证:(1)CG=BH;
(2)FC2=BF·GF;
(3)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
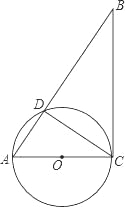
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.
(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.
(1)搅匀后从中随机摸出一球,请直接写出摸出红球的概率;
(2)如果第一次随机摸出一个球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图小方格的边长为1个单位。
(1)画出坐标系,使A、B的坐标分别为(1,1)、(-2,0),并写出点C的坐标;
(2)若将△ABC向右平移4个单位,再向上平移3个单位,得到![]() ,在图中画出
,在图中画出![]() ;
;
(3)写出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() ,直线
,直线![]() 和直线
和直线![]() 、
、![]() 交于点
交于点![]() 和
和![]() ,点
,点![]() 是直线
是直线![]() 上一动点.
上一动点.



图1 图2 图3
(1)如图1,当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() ,
,![]() ,
,![]() 之间存在什么数量关系?请你猜想结论并说明理由
之间存在什么数量关系?请你猜想结论并说明理由
(2)当点![]() 在
在![]() 、
、![]() 两点的外侧运动时(
两点的外侧运动时(![]() 点与点
点与点![]() 、
、![]() 不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出
不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出![]() ,
,![]() ,
,![]() 之间的数量关系,不必写理由.
之间的数量关系,不必写理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过________小时车库恰好停满.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com