Question

13．（1）数学课上老师提出如下问题：
如图，直线OM⊥ON，垂足为O，三角板的直角顶点C落在∠MON的内部，三角板的另两条直角边分别与ON、OM交于点D和点B．
①填空：∠OBC+∠ODC=180°；
②若DE平分∠ODC，BF平分∠CBM（如图1），试说明DE⊥BF．
请你完成上述问题．
（2）课后小佳和小芳对问题进行了进一步研究，若把DE平分∠ODC改为DG分别平分∠ODC的外角，其他条件不变（如图2），小佳和小芳发现BF与DG的位置关系发生了变化，请你判断BF与DG的位置关系，并说明理由．

Answer 1

分析 （1）①根据四边形的性质，可得答案；
②根据补角的性质，可得∠CBM=∠ODC，根据相似三角形的判定与性质，可得答案；
（2）根据直角三角形的性质，可得∠DBC+∠BDC=90，根据补角的性质，可得∠NDC+∠CBM=180，根据角的和差，可得∴∠DBC+∠BDC+∠GDC+∠FBC=180
°，根据平行线的判定，可得答案．

解答 解：（1）①由四边形内角的性质，得
∠OBC+∠ODC=180°，
故答案为：180．
②如图1
，
延长DE交BF于G，
∵∠ODC+∠OBC=∠CBM+∠OBC=180，
∴∠CBM=∠ODC，
$\frac{1}{2}$∠CBM=∠EBG=$\frac{1}{2}$∠ODC=∠EDC．
∵∠BEG=∠DEC，
∴△DEC∽△BEG，
∴∠BGE=∠DCE=90°
所以DE垂直BF
（2）平行，理由如下：
连接BD，如图2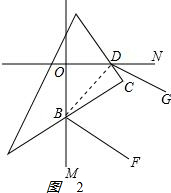
，
∵∠BCD=90°，
∴∠DBC+∠BDC=90°．
∵∠ODC=∠CBM，
∠NDC+∠ODC=180°，∠NDC+∠CBM=180°，
∵∠GDC+∠FBC=$\frac{1}{2}$∠NDC+$\frac{1}{2}$∠CBM=90°，
∴∠DBC+∠BDC+∠GDC+∠FBC=180°，
即∠DBF+∠BDG=180°，
∴DG∥BF．

点评 本题考查了三角形的内角和定理，利用相似三角形的判定与性质是解题关键；利用补角的性质得出∠NDC+∠CBM=180°是解题关键．