
分析 根据题意,$\sqrt{25-{x}^{2}}$-$\sqrt{15-{x}^{2}}$=2,变形为$\sqrt{25-{x}^{2}}$=$\sqrt{15-{x}^{2}}$+2,两边平方得x2=$\frac{51}{4}$,代入求值即可.
解答 解:∵$\sqrt{25-{x}^{2}}$-$\sqrt{15-{x}^{2}}$=2,
∴$\sqrt{25-{x}^{2}}$=$\sqrt{15-{x}^{2}}$+2,
两边平方得,25-x2=4+15-x2+4$\sqrt{15-{x}^{2}}$,
∴2$\sqrt{15-{x}^{2}}$=3,
两边平方得4(15-x2)=9,
化简,得x2=$\frac{51}{4}$,
∴$\sqrt{25-{x}^{2}}$+$\sqrt{15-{x}^{2}}$=$\frac{7}{2}$+$\frac{3}{2}$=5.
故答案为:5.
点评 本题考查了二次根式的化简求值,根据二次根式的乘除法法则进行二次根式有理化.所以一般二次根式的有理化因式是符合平方差公式的特点的式子.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
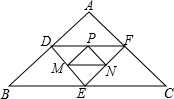 如图,点D、E、F分别是△ABC中AB、BC、AC边上的中点,点M、N、P分别是DE、EF、DF的中点.若△ABC的周长为24,则△PMN的周长为( )
如图,点D、E、F分别是△ABC中AB、BC、AC边上的中点,点M、N、P分别是DE、EF、DF的中点.若△ABC的周长为24,则△PMN的周长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,4) | B. | (-1,5 ) | C. | (-1,-3) | D. | (-3,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以点O为圆心,以OB为半径画弧,交正半轴于点C,则点C对应的数为( )
如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以点O为圆心,以OB为半径画弧,交正半轴于点C,则点C对应的数为( )| A. | 3 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年龄组 | 13岁 | 14岁 | 15岁 | 16岁 |
| 参赛人数 | 5 | 19 | 12 | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com