
分析 (1)根据二次根式乘法的法则计算即可求解;
(2)先化简,再计算加减法;
(3)根据二次根式的性质化简即可;
(4)根据平方差公式和完全平方公式计算即可求解;
(5)先化简,再计算加减法;
(6)变形为[($\sqrt{6}$+$\sqrt{5}$)($\sqrt{6}$-$\sqrt{5}$)]2006($\sqrt{6}$+$\sqrt{5}$)简便计算;
(7)根据二次根式乘除法的法则计算即可求解;
(8)先化简,再根据二次根式乘法的法则计算即可求解.
解答 解:(1)$\sqrt{(-144)×(-169)}$
=12×13
=156;
(2)$\sqrt{0.5}+\sqrt{32}-2\sqrt{\frac{1}{3}}-\sqrt{\frac{1}{8}}-\sqrt{75}$
=$\frac{\sqrt{2}}{2}$+4$\sqrt{2}$-$\frac{2\sqrt{3}}{3}$-$\frac{\sqrt{2}}{4}$-5$\sqrt{3}$
=$\frac{17\sqrt{2}}{4}$-$\frac{17\sqrt{3}}{3}$;
(3)$\sqrt{18{m^2}n}$=-3m$\sqrt{2n}$(m<0,n>0);
(4)$(3\sqrt{2}+\sqrt{3}-\sqrt{5})(3\sqrt{2}-\sqrt{3}+\sqrt{5})$
=[3$\sqrt{2}$+($\sqrt{3}$-$\sqrt{5}$)][3$\sqrt{2}$-($\sqrt{3}$-$\sqrt{5}$)]
=18-($\sqrt{3}$-$\sqrt{5}$)2
=18-3+2$\sqrt{15}$-5
=10+2$\sqrt{15}$;
(5)$\sqrt{45}+\sqrt{18}-\sqrt{8}+\sqrt{125}$
=3$\sqrt{5}$+3$\sqrt{2}$-2$\sqrt{2}$+5$\sqrt{5}$
=8$\sqrt{5}$+$\sqrt{2}$;
(6)${(\sqrt{6}+\sqrt{5})^{2007}}×{(\sqrt{6}-\sqrt{5})^{2006}}$
=[($\sqrt{6}$+$\sqrt{5}$)($\sqrt{6}$-$\sqrt{5}$)]2006($\sqrt{6}$+$\sqrt{5}$)
=(6-5)2006($\sqrt{6}$+$\sqrt{5}$)
=1×($\sqrt{6}$+$\sqrt{5}$)
=($\sqrt{6}$+$\sqrt{5}$);
(7)$\sqrt{1\frac{2}{3}}÷\sqrt{2\frac{1}{3}}×\sqrt{1\frac{2}{5}}$
=$\sqrt{\frac{5}{3}×\frac{3}{7}×\frac{7}{5}}$
=1;
(8)$3\sqrt{8}×(\sqrt{54}-5\sqrt{2}-2\sqrt{6})$
=6$\sqrt{2}$×(3$\sqrt{6}$-5$\sqrt{2}$-2$\sqrt{6}$)
=6$\sqrt{2}$×($\sqrt{6}$-5$\sqrt{2}$)
=12$\sqrt{3}$-60.
点评 考查了二次根式的混合运算,注意二次根式的运算结果要化为最简二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $-\sqrt{3}+2$ | D. | $\sqrt{3}$+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一只蚂蚁在某公园的位置平面图上爬行,它从西门出发,沿北偏东60°的方向爬行400cm到达望春亭,在望春亭停留片刻,小蚂蚁又沿北偏西60°的方向爬行400cm到达中心广场.
如图,一只蚂蚁在某公园的位置平面图上爬行,它从西门出发,沿北偏东60°的方向爬行400cm到达望春亭,在望春亭停留片刻,小蚂蚁又沿北偏西60°的方向爬行400cm到达中心广场.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
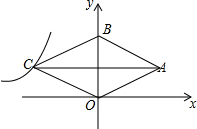 菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
菱形OABC的顶点O为原点,顶点B在y轴上,菱形的两条对角线的长分别是8和6(AC>BO),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )| A. | 12 | B. | 24 | C. | -12 | D. | -24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com