
如图,已知∆ABC是等边三角形,边长为10,点D、E、F分别在边AB、BC、AC上,且AD=BE=CF,
(1)设AD为x,△ADF的面积为y,当x为何值时,△ADF的面积最大,最大面积是多少?
(2)当x为何值时,△ADF是直角三角形?

解:(1)因为AD为x,AD=BE=CF,所以AF=10-x……………1分
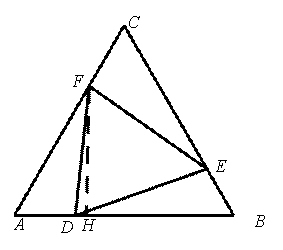 过F作AB的垂线,垂足为H……………2分
过F作AB的垂线,垂足为H……………2分
因为∆ABC是等边三角形,所以∠A=60°,则FH=AF×sin60°=(10-x)× …………3分
…………3分
所以y= (10-x) ×
(10-x) × =-
=- +5x……………4分
+5x……………4分
所以x=-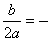
 =
= =
= ……………5分
……………5分
y=- +5×
+5× =-
=- +
+ =
= ……………6分
……………6分
所以当x= ,△ADF的面积最大,最大面积是
,△ADF的面积最大,最大面积是 平方单位……………7分
平方单位……………7分
(2)如果△ADF是直角三角形,令∠ADF是直角根据勾股定理的逆定理得: +
+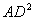 =
=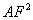
则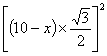 +
+ =
=
解得: (舍去),
(舍去),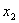 =
= ……………8分
……………8分
如果△ADF是直角三角形,令∠AFD是直角,根据勾股定理的逆定理得: +
+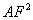 =
=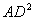
则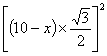 +
+ =
= ,此方程无实数解
,此方程无实数解 ……………9分
……………9分
所以当x= 时,△ADF是直角三角形. ……………10分
时,△ADF是直角三角形. ……………10分


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元,设平均每次降价的百分率为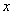 ,则下面所列方程正确的是( )
,则下面所列方程正确的是( )
A、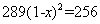 B、
B、 C、
C、 D、
D、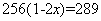
查看答案和解析>>
科目:初中数学 来源: 题型:
2010年10月9日,国家发改委价格司公布《关于居民生活用电实行阶梯电价的指导意见》提供了两套可供选择的电价方案,向社会公开征求意见:
方案一:第一档月均用电量110度以内,该档内电价不变动;第二档月用电量为110度至210度,提价标准不低于每度5分钱;第三档为用电量210度以上,每度电价上调不低于0.2元。
方案二,第一档电价月用电量140度以内每度提高1分钱;第二档月均用电量为140度至270度,每度电价提高不低于5分钱;第三档为用电量270度以上,每度电价提高不低于0.2元。
为此某单位组织了一次调查,同意方案一的人数用A表示,同意方案二的人数用B表示,认为是变相涨价的人数用C表示,无所谓的人数用D表示,并根据统计情况制作了统计图表。请根据统计图表提供的信息回答下列问题:
(1)该单位共调查了多少人?并补全条形统计图;
(2)在圆中表示D的扇形的圆心角是多少度?
(3)为什么会有30%的人认为变相涨价?

查看答案和解析>>
科目:初中数学 来源: 题型:
下列事件是必然事件的是( )
A.通常加热到100℃,水沸腾;
B.抛一枚硬币,正面朝上;
C.明天会下雨;
D.经过城市中某一有交通信号灯的路口,恰好遇到红灯.
|
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在四边形ABCD中,对角线AC、BD互相垂直,点E、F、G、H分别是边AB、BC、CD、DA的中点,依次连结这四个中点得到四边形EFGH.
(1)求证:四边形EFGH是矩形;
(2)若AC=15,BD=10,求四边形EFGH的周长.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com