
【题目】已知:在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 、
、![]() 轴于点A、B两点,OA=5,∠OAB=60°.
轴于点A、B两点,OA=5,∠OAB=60°.
(1)如图1,求直线AB的解析式;
(2)如图2,点P为直线AB上一点,连接OP,点D在OA延长线上,分别过点P、D作OA、OP的平行线,两平行线交于点C,连接AC,设AD=m,△ABC的面积为S,求S与m的函数关系式;
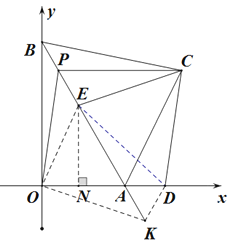
(3)如图3,在(2)的条件下,在PA上取点E ,使PE=AD, 连接EC,DE,若∠ECD=60°,四边形ADCE的周长等于22,求S的值.

【答案】(1)直线解析式为![]() ;(2)S=
;(2)S=![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出点B坐标,设AB解析式为![]() ,把点A(5,0),B(0,
,把点A(5,0),B(0,![]() )分别代入,利用待定系数法进行求解即可;
)分别代入,利用待定系数法进行求解即可;
(2)由题意可得四边形ODCP是平行四边形,∠OAB=∠APC=60°,则有PC=OD=5+m,∠PCH=30°,过点C作CH⊥AB,在Rt△PCH中 利用勾股定理可求得CH=![]() ,再由S=
,再由S=![]() AB
AB![]() CH代入相关数据进行整理即可得;
CH代入相关数据进行整理即可得;
(3) 先求得∠PEC=∠ADC,设∠OPA=![]() ,则∠OPC= ∠ADC= ∠PEC=60°+
,则∠OPC= ∠ADC= ∠PEC=60°+![]() ,在BA延长线上截取AK=AD,连接OK,DK,DE,证明△ADK是等边三角形,继而证明△PEC≌△DKO,通过推导可得到OP=OK=CE=CD,再证明△CDE是等边三角形,可得CE=CD=DE,连接OE,证明△OPE≌△EDA,继而可得△OAE是等边三角形,得到OA=AE=5 ,根据四边形ADCE的周长等于22,可得ED=
,在BA延长线上截取AK=AD,连接OK,DK,DE,证明△ADK是等边三角形,继而证明△PEC≌△DKO,通过推导可得到OP=OK=CE=CD,再证明△CDE是等边三角形,可得CE=CD=DE,连接OE,证明△OPE≌△EDA,继而可得△OAE是等边三角形,得到OA=AE=5 ,根据四边形ADCE的周长等于22,可得ED=![]() ,过点E作EN⊥OD于点N,则DN=
,过点E作EN⊥OD于点N,则DN=![]() ,由勾股定理得
,由勾股定理得![]() , 可得关于m的方程,解方程求得m的值后即可求得答案.
, 可得关于m的方程,解方程求得m的值后即可求得答案.
(1)在Rt△ABO中OA=5,∠OAB=60°,
∴∠OBA=30°,AB=10 ,
由勾股定理可得OB=![]() ,
,
∴B(0,![]() ),
),
设AB解析式为![]() ,把点A(5,0),B(0,
,把点A(5,0),B(0,![]() )分别代入,得
)分别代入,得 ,
,
∴ ,
,
∴直线解析式为![]() ;
;
(2)∵CP//OD,OP//CD,
∴四边形ODCP是平行四边形,∠OAB=∠APC=60°,
∴PC=OD=5+m,∠PCH=30°,
过点C作CH⊥AB,在Rt△PCH中 PH=![]() ,由勾股定理得CH=
,由勾股定理得CH=![]() ,
,
∴S=![]() AB
AB![]() CH=
CH=![]() ;
;
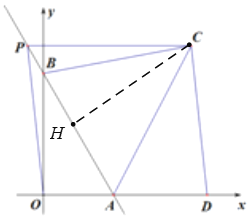
(3) ∵∠ECD=∠OAB=60°,
∴∠EAD+∠ECD=180°,∠CEA+∠ADC=180°,
∴∠PEC=∠ADC,
设∠OPA=![]() ,则∠OPC= ∠ADC= ∠PEC=60°+
,则∠OPC= ∠ADC= ∠PEC=60°+![]() ,
,
在BA延长线上截取AK=AD,连接OK,DK,DE,
∵∠DAK=60°,
∴△ADK是等边三角形,
∴AD=DK=PE,∠ODK=∠APC,
∵PC=OD,
∴△PEC≌△DKO,
∴OK=CE,∠OKD=∠PEC=∠OPC=60°+![]() , ∠AKD= ∠APC=60° ,
, ∠AKD= ∠APC=60° ,
∴∠OPK= ∠OKB,
∴OP=OK=CE=CD,
又∵∠ECD=60°,
∴△CDE是等边三角形,
∴CE=CD=DE,
连接OE,∵ ∠ADE=∠APO,DE=CD=OP,
∴△OPE≌△EDA,
∴AE=OE, ∠OAE=60°,
∴△OAE是等边三角形,
∴OA=AE=5 ,
∵四边形ADCE的周长等于22,
∴AD+2DE=17,
∴ED=![]() ,
,
过点E作EN⊥OD于点N,则DN=![]() ,
,
由勾股定理得![]() ,
,
即![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴S=![]() =20
=20![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小利同学调查了全班50名同学分别喜欢相声、小品、歌曲、舞蹈节目的情况,并制成下面的统计表:
最喜欢的节目的类别 | 划记 | 人数 | 百分比(%) |
相声 | 正 | 9 | 12 |
小品 | 正正正 | 21 | 42 |
歌曲 | 正正 | 10 | 28 |
舞蹈 | 正 | 6 | 12 |
在表中的数据中,仅有一类节目的统计是完全正确的,则该项统计类别是( )
A. 相声B. 舞蹈C. 歌曲D. 小品
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知直线y=-![]() x+4与y轴交于A点,与x轴交于B点,C点坐标为(﹣2,0).
x+4与y轴交于A点,与x轴交于B点,C点坐标为(﹣2,0).
(1)求经过A,B,C三点的抛物线的解析式;
(2)如果M为抛物线的顶点,联结AM、BM,求四边形AOBM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
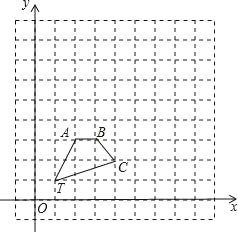
【题目】如图,在正方形网格中,四边形TABC的顶点坐标分别为T(1,1),A(2,3),B(3,3),C(4,2).
(1)以点T(1,1)为位似中心,在位似中心的同侧将四边形TABC放大为原来的2倍,放大后点A,B,C的对应点分别为A′,B′,C′画出四边形TA′B′C′;
(2)写出点A′,B′,C′的坐标:
A′ ,B′ ,C′ ;
(3)在(1)中,若D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点 O 按如图方式叠放在一起.
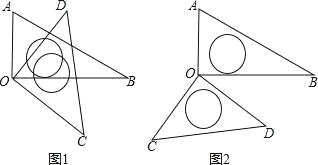
( 1 ) 如图 1 , 若∠ BOD=35° , 则∠ AOC= ; 若∠AOC=135°, 则∠BOD= ;
(2)如图2,若∠AOC=140°,则∠BOD= ;
(3)猜想∠AOC 与∠BOD 的大小关系,并结合图1说明理由.
(4)三角尺 AOB 不动,将三角尺 COD 的 OD 边与 OA 边重合,然后绕点 O 按顺时针或逆时针方向任意转动一个角度,当∠A OD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD 角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师给同学们布置了一道社会实践题,收集并统计本地区一周内的最高气温和最低气温.小明根据收集到的数据列出了表格:
星期天 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | |
最高气温(℃) | +5 | +6 | +4 | +1 | +1 | +3 | +3 |
最低气温(℃) | +1 | +3 | +1 | ﹣3 | ﹣4 | ﹣3 | ﹣2 |
(1)本周内当地最高气温和最低气温分别是多少℃?
(2)在这一周中,哪一天的温差最大?最大温差是多少?
(3)这一周的最低气温的平均数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,使点C落在点C′的位置,BC′交AD于点G(图1);再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M(图2),则EM的长为( )
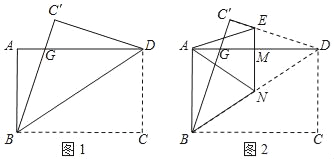
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com