Question

20．如图，直线y=-x-1与双曲线$y=\frac{-2}{x}$交于A、B两点．
（1）求A、B两点的坐标．
（2）根据图象写出一次函数的值大于反比例函数的值的x的取值范围．
（3）连接OA、OB，求△AOB的面积．

Answer 1

分析 （1）直接联立两函数的解析式即可得出A、B两点的坐标；
（2）直接利用函数图象即可得出结论；
（3）求出C点坐标，根据S_△OAB=S_△OAC+S_△OBC即可得出结论．

解答 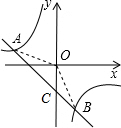解：（1）由$\left\{\begin{array}{l}y=-x-1\\ y=\frac{-2}{x}\end{array}\right.$得  $\left\{\begin{array}{l}{x_1}=-2\\{y_1}=1\end{array}\right.$，$\left\{\begin{array}{l}{x_2}=1\\{y_2}=-2\end{array}\right.$
故A（-2，1），B（1，-2）；

（2）由函数图象可知，x＜-2或0＜x＜1时，一次函数的值大于反比例函数的值；

（3）设直线y=-x-1与y轴交于C，则C（0，-1）
S_△OAB=S_△OAC+S_△OBC=$\frac{1}{2}×1×2+\frac{1}{2}×1×1$=$\frac{3}{2}$．

点评 本题考查的是反比例函数与一次函数的交点问题，根据题意求出A、B两点的坐标是解答此题的关键．