
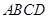 中,
中, 厘米,
厘米,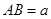 厘米(
厘米(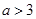 ).动点
).动点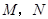 同时从
同时从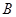 点出发,分别沿
点出发,分别沿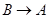 ,
,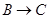 运动,速度是
运动,速度是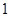 厘米/秒.过
厘米/秒.过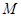 作直线垂直于
作直线垂直于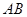 ,分别交
,分别交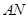 ,
,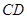 于
于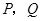 .当点
.当点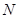 到达终点
到达终点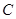 时,点
时,点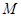 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为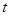 秒.
秒.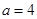 厘米,
厘米,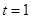 秒,则
秒,则 ______厘米;
______厘米;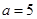 厘米,求时间
厘米,求时间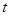 ,使
,使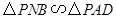 ,并求出它们的相似比;
,并求出它们的相似比;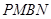 与梯形
与梯形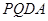 的面积相等,求
的面积相等,求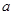 的取值范围;
的取值范围;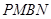 ,梯形
,梯形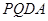 ,梯形
,梯形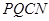 的面积都相等?若存在,求
的面积都相等?若存在,求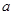 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.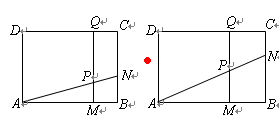
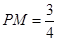 ,
,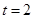 ,使
,使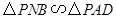 ,相似比为
,相似比为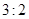
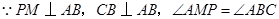 ,
,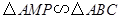 ,
,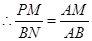 即
即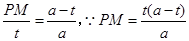 ,
,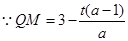
 与梯形
与梯形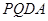 的面积相等,即
的面积相等,即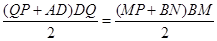
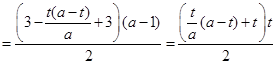 化简得
化简得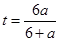 ,
,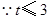 ,
,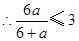 ,则
,则 ,
, 时,梯形
时,梯形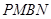 与梯形
与梯形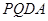 的面积相等
的面积相等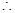 梯形
梯形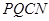 的面积与梯形
的面积与梯形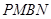 的面积相等即可,则
的面积相等即可,则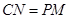
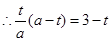 ,把
,把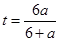 代入,解之得
代入,解之得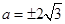 ,所以
,所以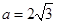 .
.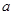 ,当
,当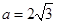 时梯形
时梯形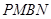 与梯形
与梯形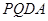 的面积、梯形
的面积、梯形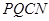 的面积相等.
的面积相等.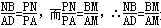 这样就可以求出t,也可以求出相似比;
这样就可以求出t,也可以求出相似比;

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.AB︰ED=5︰3 | B.△EDC与△ABC的周长比为5︰8 |
| C.△EDC与△ABC的面积比为25︰64 | D.△BED与△EDC的面积比为3︰5 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 。(说明:顶点都在网格线交点处的三角形叫做格点三角形。友情提示:请在画出的三角形的项点处标上相对应的字母!)
。(说明:顶点都在网格线交点处的三角形叫做格点三角形。友情提示:请在画出的三角形的项点处标上相对应的字母!)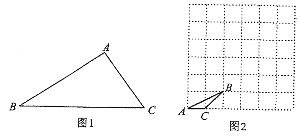
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
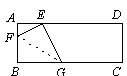
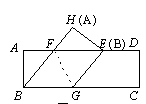
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com