
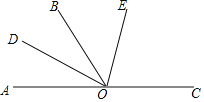
【题目】如图所示,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内.
(1)若OE平分∠BOC,则∠DOE等于多少度?
(2)若∠BOE=![]() ∠EOC,∠DOE=60°,则∠EOC是多少度?
∠EOC,∠DOE=60°,则∠EOC是多少度?
【答案】(1)∠DOE=90°;(2)∠EOC =90°.
【解析】
(1)根据角平分线定义和角的和差即可得到结论;
(2)设∠AOB=x,则∠BOC=180°-x,根据角平分线的定义得到∠BOD=![]() ∠AOB=
∠AOB=![]() x,列方程即可得到结论.
x,列方程即可得到结论.
解:(1)∵OD平分∠AOB,OE平分∠BOC,
∴∠BOD=![]() ∠AOB,∠BOE=
∠AOB,∠BOE=![]() ∠BOC,
∠BOC,
∴∠DOE=∠BOD+∠BOE=![]() (∠AOB+∠BOC)=
(∠AOB+∠BOC)=![]() ×180°=90°;
×180°=90°;
(2)∵∠BOE=![]() ∠EOC,
∠EOC,
∴∠BOE=![]() ∠BOC,
∠BOC,
设∠AOB=x,则∠BOC=180°-x,
∵OD平分∠AOB,
∴∠BOD=![]() ∠AOB=
∠AOB=![]() x,
x,
∵∠BOE=![]() ∠BOC=45°-
∠BOC=45°-![]() x,
x,
∴∠DOE=∠BOD+∠BOE=![]() x+45°-
x+45°-![]() x=60°,
x=60°,
∴x=60°,
∴∠AOB=60°,
∴∠BOC=120°,
∴∠EOC=![]() ∠BOC=90°.
∠BOC=90°.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
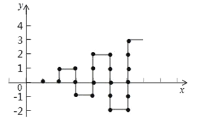
【题目】如图,在平面直角坐标系中,有若干个整数点(横、纵坐标均为整数),其顺序按图中方向排列,如 1, 0 ,2, 0 , 2,1 , 3,1 , 3, 0 ……根据这个规律探索可得,第 2019 个点的坐标为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生的课余生活,陶冶学生的情操,促进学生全面发展,某中学七年级开展了学生社团活动,学校为了解学生参加情况,对部分学生进行了调查,制作出如下的统计图:

请根据统计图,完成以下问题:
(1)这次共调查了 名学生;在扇形统计图中,表示“书法类”所在扇形的圆心角是 度.
(2)请把统计图1 补充完整.
(3)若七年级共有学生1100 名,请估算有多少名学生参加文学类社团.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太麻烦,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果:
1+2+3+4+5+…+100
=(1+100)+(2+99)+(3+98)+…+(50+51)
=101× = .
(1)补全例题解题过程;
(2)请猜想:1+2+3+4+5+6+…+(2n﹣2)+(2n﹣1)+2n= .
(3)试计算:a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在学习《从面积到乘法公式》时,曾用两种不同的方法计算同一个图形的面积,探索了单项式乘多项式的运算法则:m(a+b+c)=ma+mb+mc(如图1),多项式乘多项式的运算法则:
(a+b)(c+d)=ac+ad+bc+bd(如图2),以及完全平方公式:(a+b)2=a2+2ab+b2(如图3).
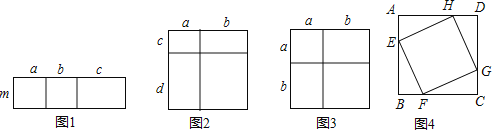
把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式,这是研究数学问题的一种常用方法.
(1)请设计两个图形说明一下两个等式成立(画出示意图,并标上字母)
①(a+b)(2a+b)=2a2+3ab+b2
②(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(2)如图4,它是由四个形状、大小完全相同的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD.如果每个直角三角形的较短的边长为a,较长的边长为b,最长的边长为c.试用两种不同的方法计算这个大正方形的面积,你能发现直角三角形的三边长a、b、c的什么数量关系?(注:写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天) | 豪华间(元/人/天) | 贵宾间(元/人/天) | |
三人间 | 50 | 100 | 500 |
双人间 | 70 | 150 | 800 |
单人间 | 100 | 200 | 1500 |
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com