
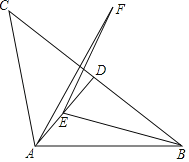
【题目】 如图,△ABC中,AB=AC,∠ABC=α,tanα=![]() ,AD⊥BC于点D,点E是线段AD上的一个动点,连接EB,将线段EB绕点E逆时针旋转2α后得到线段EF,连接AF,若BC=24,则线段AF的最小值为_____.
,AD⊥BC于点D,点E是线段AD上的一个动点,连接EB,将线段EB绕点E逆时针旋转2α后得到线段EF,连接AF,若BC=24,则线段AF的最小值为_____.
【答案】![]()
【解析】
连接BF,过点E作EH⊥BF于H,作![]() ,在BT上取一点使得AT=BT,连接AT,TE,过点T作TG⊥AB于G,证明
,在BT上取一点使得AT=BT,连接AT,TE,过点T作TG⊥AB于G,证明![]() ∽
∽![]() ,推出
,推出![]() =
=![]() =
=![]() ,得到AF=
,得到AF=![]() TE,求出TE的最小值即可解决问题.
TE,求出TE的最小值即可解决问题.
解:如图,连接BF,过点E作EH⊥BF于H,作![]() ,在BT上取一点使得AT=BT,连接AT,TE,过点T作TG⊥AB于G,
,在BT上取一点使得AT=BT,连接AT,TE,过点T作TG⊥AB于G,
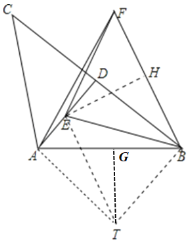
∵BE=EF,EH⊥BF,∠BEF=2α,
∴∠BEH=∠FEH=α,∠BHE=90°,BH=FH,
∴∠EBF+∠BEH=∠EBF+α=90°,
∵AB=AC,AD⊥BC,
∴∠BAD+∠ABD=90°,即∠BAD+α=90°,
∴∠EBF=∠BAD,
∵AD∥BT,
∴∠ABT=∠BAD,
∴∠ABT=∠EBF,
∴∠ABT+∠ABE=∠EBF+∠ABE,即∠TBE=∠ABF,
∵TG⊥AB于G,
∴∠ABT+∠BTG=90°,
又∵∠EBF+∠BEH=90°,
∴∠BTG=∠BEH=α,
∵tanα=![]() ,
,
∴tan∠BEH=![]() =
=![]() ,设BH=5k,EH=6k,则BF=10k,BE=
,设BH=5k,EH=6k,则BF=10k,BE=![]() k,
k,
∴![]() =
=![]() =
=![]() ,
,
∵TA=TB,TG⊥AB,
∴AG=BG,
∵tan∠ABD=![]() =
=![]() ,
,
∴设AD=5m,BD=6m,则AB=![]() m,AG=BG=
m,AG=BG=![]() m,
m,
又∵tan∠BTG=![]() =
=![]() ,
,
∴TG=![]() m,则BT=
m,则BT=![]() m,
m,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠TBE=∠ABF,
∴![]() ∽
∽![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴AF=![]() TE,
TE,
∵CD=DB=12,tan∠ABC=![]() =
=![]() ,
,
∴AD=10,AB=![]() =
=![]() =
=![]() ,
,
∴BT=AT=![]() ,
,
∵ET最小时,AF的值最小,观察图象可知当E与A重合时,ET的值最小,最小值为![]() ,
,
∴AF的最小值=![]() .
.
故答案为:![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD,过点D作PD∥BC与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:BD2=PBAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列分式方程解应用题:
“5G改变世界,5G创造未来”.2019年9月,全球首个5G上海虹桥火车站,完成了5G网络深度覆盖,旅客可享受到高速便捷的5G网络服务.虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍.在峰值速率下传输7千兆数据,5G网络比4G网络快630秒,求5G网络的峰值速率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠疫情初期,医用口罩是紧缺物资.某市为降低因购买口罩造成人群聚集的感染风险,通过APP实名预约,以摇号抽签的方式,由市民到指定门店购买口罩.规定:已中签者在本轮摇号结束前不再参与摇号;若指定门店当日市民购买口罩的平均等待时间超过8分钟,则次日必须增派工作人员.
(1)据APP数据统计:第一天有386.5万人进行网上预约,此后每天预约新增4万人,且每天有35.5万人中签,若小明第一天没有中签,则他第二天中签的概率是多少?
(2)该市某区指定A,B两门店每天8:00-22:00时段让中签市民排队购买口罩.图1是A门店某日购买口罩的人数与等待时间的统计图,为了算出A门店某日等待9分钟的人数,小红选择14:00~16:00这个时间段到店进行统计,统计结果见表1,且这个时间段的人数占该店当天等待9分钟人数的![]() .表2是B门店某日购买口罩的人数与等待时间的统计表.请你运用所学的统计知识判断A,B门店次日是否需要增派工作人员.
.表2是B门店某日购买口罩的人数与等待时间的统计表.请你运用所学的统计知识判断A,B门店次日是否需要增派工作人员.
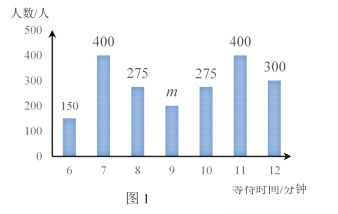
表1
时间段 | 等待9分钟/人 |
14:00~14:30 | 10 |
14:30~15:00 | 20 |
15:00~15:30 | 15 |
15:30~16:00 | 5 |
表2
等待时间 |
|
|
|
|
人数/人 |
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.

(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平面直角坐标系中,直线y1=kx+b与x轴交于点A(4,0),与y轴交于点B(0,3),点C是直线y2=![]() x+5上的一个动点,连接BC,过点C作CD⊥AB于点D.
x+5上的一个动点,连接BC,过点C作CD⊥AB于点D.
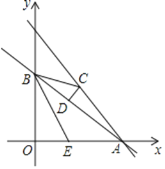
(1)求直线y1=kx+b的函数表达式;
(2)当BC∥x轴时,求BD的长;
(3)点E在线段OA上,OE=![]() OA,当点D在第一象限,且△BCD中有一个角等于∠OEB时,请直接写出点C的横坐标.
OA,当点D在第一象限,且△BCD中有一个角等于∠OEB时,请直接写出点C的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里,装有若干个完全相同的A、B、C三种球,其中A球x个,B球x个,C球(x+1)个.若从中任意摸出一个球是A球的概率为0.25.
(1)这个袋中A、B、C三种球各多少个?
(2)若小明从口袋中随机模出1个球后不放回,再随机摸出1个.请你用画树状图的方法求小明摸到1个A球和1个C球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了防范疫情,顺利复学,某市教育局决定从甲、乙两地用汽车向![]() 两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,
两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,![]() 两校分别需要口罩30万个,20万个,两地到
两校分别需要口罩30万个,20万个,两地到![]() 两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
路程 | 路程 | |
甲地 | 乙地 | |
A校 | 10 | 20 |
B校 | 15 | 15 |
(1)根据题意,在答题卡中填写下表:
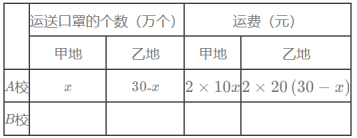
(2)设总运费为![]() 元,求
元,求![]() 与
与![]() 的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?
的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
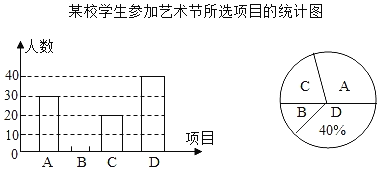
【题目】某校艺术节共开展了四项活动:器乐(A),舞蹈(B),绘画C),唱歌(D),每名学生只能参加一项活动.学校对学生所选的项目进行了抽样调查,并将调查结果绘制了如图两幅不完整的统计图,请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有 人;
(2)补全条形统计图.
(3)该校共有500名学生,请估计选择“绘画”的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com