
 如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.
如图,四边形ABCD是正方形,BM=DF,AF垂直AM,M、B、C在一条直线上,且△AEM与△AEF恰好关于AE所在直线成轴对称,已知EF=x,正方形边长为y.分析 (1)利用旋转的定义求解;
(2)由于△AEM≌△AEF,则EF=EM,即x=BE+BM=DF+BE,则根据三角形面积公式得到S△AME=$\frac{1}{2}$xy,然后利用S△CEF=S正方形ABCD-S△AEF-S△ABE-S△ADF可表示出△EFC的面积.
解答 解:(1)图中△ADF可以绕点A按顺时针方向旋转90°后能够与△ABM重合;
故答案为:A、90°,ABM.
(2)∵△AEM与△AEF恰好关于所在直线成轴对称,
∴EF=EM,
即x=BE+BM,
∵BM=DF,
∴x=DF+BE,
∴S△AME=$\frac{1}{2}$•AB•ME=$\frac{1}{2}$xy,
S△CEF=S正方形ABCD-S△AEF-S△ABE-S△ADF
=y2-$\frac{1}{2}$xy-$\frac{1}{2}$•y•BE-$\frac{1}{2}$•y•DF
=y2-$\frac{1}{2}$xy-$\frac{1}{2}$•y(BE+DF)
=y2-$\frac{1}{2}$xy-$\frac{1}{2}$•y•x
=y2-xy.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
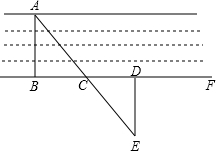 如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线,并在这条垂线上取一点E,使A、C、E在一条直线上(如图所示),测得ED的长就是A、B之间的距离,请你说明理由.
如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线,并在这条垂线上取一点E,使A、C、E在一条直线上(如图所示),测得ED的长就是A、B之间的距离,请你说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 优惠 条件 | 一次性购物不超过200元 | 一次性购物超过200元,但不超过500元 | 一次性购物超过500元 |
| 优惠 办法 | 没有优惠 | 全部按九折优惠 | 其中500元仍按九折优惠,超过500元部分按八折优惠 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
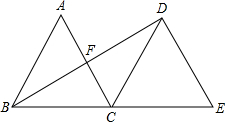 如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.求线段BD的长.
如图,△ABC是边长为2的等边三角形,将△ABC沿直线BC向右平移,使点B与点C重合,得到△DCE,连接BD,交AC于点F.求线段BD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
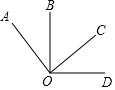 如图,以点O为端点按顺时针方向依次作射线OA、OB、OC、OD,且∠AOC=∠BOD=α(0°<α<180°)
如图,以点O为端点按顺时针方向依次作射线OA、OB、OC、OD,且∠AOC=∠BOD=α(0°<α<180°)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com