练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

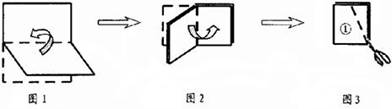
    . 取一张矩形纸片按照图1、图2中的方法对折，并沿图3中过矩形顶点的斜线（虚线）剪开，把剪下的①这部分展开，平铺在桌面上．若平铺的这个图形是正六边形，则这张矩形纸片的宽和长之比为             .


     

    解析:解：作OB⊥AD，根据已知可以画出图形，

    ∵根据折叠方式可得：

    AB=AD，CD=CE，∠OAB=60°，AO等于正六边形的边长，

    ∴∠BOA=30°，

    ∴2AB=AO，

    =tan60°=，

    ∴BO：AM=：2．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    小华将一张矩形纸片（如图1）沿对角线CA剪开，得到两张三角形纸片（如图2），其中∠ACB=α，然后将这两张三角形纸片按如图3所示的位置摆放，△EFD纸片的直角顶点D落在△ACB纸片的斜边AC上，直角边DF落在AC所在的直线上．
    （1）若ED与BC相交于点G，取AG的中点M，连接MB、MD，当△EFD纸片沿CA方向平移时（如图3），请你观察、测量MB、MD的长度，猜想并写出MB与MD的数量关系，然后证明你的猜想；
    （2）在（1）的条件下，求出∠BMD的大小（用含α的式子表示），并说明当α=45°时，△BMD是什么三角形；
    （3）在图3的基础上，将△EFD纸片绕点C逆时针旋转一定的角度（旋转角度小于90°），此时△CGD变成△CHD，同样取AH的中点M，连接MB、MD（如图4），请继续探究MB与MD的数量关系和∠BMD的大小，直接写出你的猜想，不需要证明，并说明α为何值时，△BMD为等边三角形．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将一张矩形纸片（如图a）沿对角线AC剪开，得到两张三角形纸片（如图b），其中∠ACB=α，然后将这两张三角形纸片按如图c所示的位置摆放，△EFD纸片的直角顶点D落在△ACB纸片的斜边AC上，直角边DF落在AC所在的直线上．
    （1）若ED与BC相交于点G，取AG的中点M，连接MB、MD，当△EFD纸片沿CA方向平移时（如图c），请你观察MB、MD的长度，猜想并写出MB与MD的数量关系，然后证明你的猜想；
    （2）在（1）的条件下，求出∠BMD的大小（用含α的代数式表示），并说明当α=45°时，△BMD是什么三角形？
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    小华将一张矩形纸片（如图1）沿对角线AC剪开，得到两张三角形纸片（如图2），其中∠ACB＝β，然后将这两张三角形纸片按如图3所示的位置摆放，△EFD纸片的直角顶点D落在△ACB纸片的斜边AC上，直角边DF落在AC所在的直线上。

    【小题1】（1）若DE与BC相交于点G，取AG的中点M，连结MB，MD，当△EFD纸片沿CA方向平移时（如图3），请你猜想并写出MB与MD的数量关系，然后证明你的猜想；（3分）
    【小题2】（2）在（1）的条件下，求出∠BMD的大小（用含β的式子表示），并说明当β＝45o时，△BMD是什么三角形；（5分）
    【小题3】（3）在图3的基础上，将△EFD纸片绕点C逆时针旋转一定的角度（小于90o），此时△CGD变成△CHD，同样取AH的中点M，连结MB，MD（如图4），请继续探究MB与MD的数量关系和∠BMD的大小，直接写出你的猜想，不证明，并说明β为何值时△BMD为等边三角形。（2分）

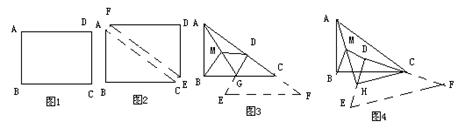
    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年浙江省杭州市余杭区星桥中学八年级第一学期期中考试数学卷 题型：解答题

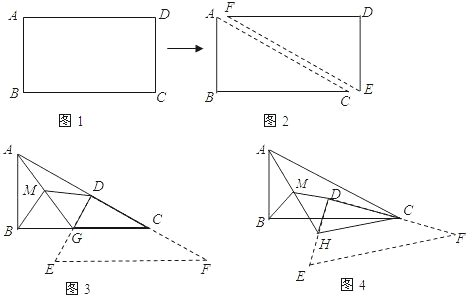
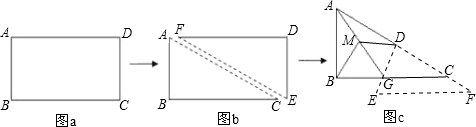
    小华将一张矩形纸片（如图1）沿对角线AC剪开，得到两张三角形纸片（如图2），其中∠ACB＝β，然后将这两张三角形纸片按如图3所示的位置摆放，△EFD纸片的直角顶点D落在△ACB纸片的斜边AC上，直角边DF落在AC所在的直线上。

    【小题1】（1）若DE与BC相交于点G，取AG的中点M，连结MB，MD，当△EFD纸片沿CA方向平移时（如图3），请你猜想并写出MB与MD的数量关系，然后证明你的猜想；（3分）
    【小题2】（2）在（1）的条件下，求出∠BMD的大小（用含β的式子表示），并说明当β＝45o时，△BMD是什么三角形；（5分）
    【小题3】（3）在图3的基础上，将△EFD纸片绕点C逆时针旋转一定的角度（小于90o），此时△CGD变成△CHD，同样取AH的中点M，连结MB，MD（如图4），请继续探究MB与MD的数量关系和∠BMD的大小，直接写出你的猜想，不证明，并说明β为何值时△BMD为等边三角形。（2分）

    查看答案和解析>>

    科目：初中数学 来源：2011-2012年浙江省杭州市八年级第一学期期中考试数学卷 题型：解答题

    小华将一张矩形纸片（如图1）沿对角线AC剪开，得到两张三角形纸片（如图2），其中∠ACB＝β，然后将这两张三角形纸片按如图3所示的位置摆放，△EFD纸片的直角顶点D落在△ACB纸片的斜边AC上，直角边DF落在AC所在的直线上。

     

     

     

     

     

     

    1.（1）若DE与BC相交于点G，取AG的中点M，连结MB，MD，当△EFD纸片沿CA方向平移时（如图3），请你猜想并写出MB与MD的数量关系，然后证明你的猜想；（3分）

    2.（2）在（1）的条件下，求出∠BMD的大小（用含β的式子表示），并说明当β＝45o时，△BMD是什么三角形；（5分）

    3.（3）在图3的基础上，将△EFD纸片绕点C逆时针旋转一定的角度（小于90o），此时△CGD变成△CHD，同样取AH的中点M，连结MB，MD（如图4），请继续探究MB与MD的数量关系和∠BMD的大小，直接写出你的猜想，不证明，并说明β为何值时△BMD为等边三角形。（2分）

     

    查看答案和解析>>

    同步练习册答案