
【题目】如图,ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE的周长为 . 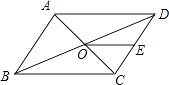
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E. 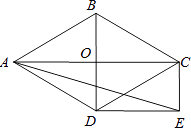
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2 ![]() 时,求sin∠AED的值.
时,求sin∠AED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.
(1)如图1,求证:AD=CD;
(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一长方形花园用来种植菊花和郁金香,其余作为休息区;
(1)求种植菊花和郁金香的面积;
(2)当![]() m,
m,![]() m时,种植菊花和郁金香的面积是多少m2?
m时,种植菊花和郁金香的面积是多少m2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
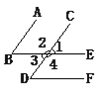
(1)如果∠1=∠B,那么_______∥_______,根据是__________________________;
(2)如果∠3=∠D,那么_______∥_______,根据是__________________________;
(3)如果要使BE∥DF,必须∠1=∠_______,根据是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD=![]() S四边形ABCD,求 P的坐标.
S四边形ABCD,求 P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:3+2=3×2-1,4+![]() =4×
=4×![]() -1,给出定义如下:
-1,给出定义如下:
我们称使等式a+b=ab-1成立的一对有理数a,b为“椒江有理数对”,记为(a,b),如:数对(3,2),(4,![]() )都是“椒江有理数对”.
)都是“椒江有理数对”.
(1)数对(-2,1),(5,![]() )中是“椒江有理数对”的是 ;
)中是“椒江有理数对”的是 ;
(2)若(a,3)是“椒江有理数对”,求a的值;
(3)若(m,n)是“椒江有理数对”,则(-n,-m) “椒江有理数对”(填“是”、“不是”或“不确定”).
(4)请再写出一对符合条件的“椒江有理数对” (注意:不能与题目中已有的“椒江有理数对”重复)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com