
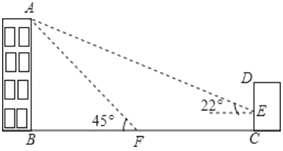
【题目】如图,某办公楼![]() 的后面有一建筑物
的后面有一建筑物![]() ,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子
,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子![]() ,而当光线与地面夹角是45°时,办公楼顶
,而当光线与地面夹角是45°时,办公楼顶![]() 在地面上的影子
在地面上的影子![]() 与墙角
与墙角![]() 有25米的距离(
有25米的距离(![]() 在一条直线上).
在一条直线上).
(1)求办公楼![]() 的高度;
的高度;
(2)若要在![]() ,
,![]() 之间挂一些彩旗,请你求出
之间挂一些彩旗,请你求出![]() ,
,![]() 之间的距离.(参考数据:
之间的距离.(参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】(1)教学楼的高20m;(2)A、E之间的距离约为48m.
【解析】
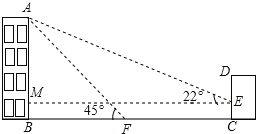
(1)如图,过点E作EM⊥AB于M,设AB为x,可得AM=x-2,ME=x+25,利用∠AEM的正切列方程求出x的值即可;
(2)利用∠AEM的余弦列方程求出AE的长即可.
如图,过点E作EM⊥AB于M,设AB为x,
Rt△ABF中,∠AFB=45°,
∴BF=AB=x,
∴ME=BC=BF+FC=x+25,
在Rt△AEM中,∠AEM=22°,AM=AB-BM=AB-CE=x-2,
tan22°=![]() ,
,
∴![]() ,
,
解得:x=20.
∴教学楼的高20m.
(2)由(1)可得ME=BC=x+25=20+25=45,
在Rt△AME中,cos22°=![]() ,
,
∴ ,
,
∴A、E之间的距离约为48m.


科目:初中数学 来源: 题型:
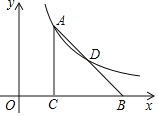
【题目】如图,在平面直角坐标系中,在Rt△ABC中,∠ACB=90°,边BC在x轴上,点B在点C的右侧,顶点A和AB的中点D在函数![]() 的图象上.若△ABC的面积为12,则k的值为( )
的图象上.若△ABC的面积为12,则k的值为( )
A.24B.12C.6D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
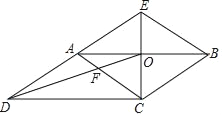
【题目】如图,CE是□ABCD的边AB的垂直平分线,垂足为点O,CE与DA的延长线交于点E、连接AC,BE,DO,DO与AC交于点F,则下列结论:①四边形ACBE是菱形;②∠ACD=∠BAE;③AF:BE=2:3;④S四边形AFOE:S△COD=2:3.其中正确的结论有( )个.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 和抛物线
和抛物线![]() (n为正整数).
(n为正整数).
(1)抛物线![]() 与x轴的交点坐标为 .顶点坐标为 .
与x轴的交点坐标为 .顶点坐标为 .
(2)当n=1时,请解答下列问题:
①抛物线![]() 与x轴的交点坐标为 .顶点坐标为 .请写出抛物线y,
与x轴的交点坐标为 .顶点坐标为 .请写出抛物线y,![]() 的一条相同的性质.
的一条相同的性质.
②当直线![]() 与抛物线y,
与抛物线y,![]() ,共有4个交点时,求m的取值范围
,共有4个交点时,求m的取值范围
(3)若直线y=k(k<0)与抛物线y,![]() 共有4个交点,从左至右依次标记为点A,B,C,D,当AB=BC=CD时,求出k,n之间满足的关系式.
共有4个交点,从左至右依次标记为点A,B,C,D,当AB=BC=CD时,求出k,n之间满足的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ,与x轴交于A、B两点(点A在点B的左侧).
,与x轴交于A、B两点(点A在点B的左侧).
(1)求点A和点B的坐标;
(2)若点P(m,n)是抛物线上的一点,过点P作x轴的垂线,垂足为点D.
①在![]() 的条件下,当
的条件下,当![]() 时,n的取值范围是
时,n的取值范围是![]() ,求抛物线的表达式;
,求抛物线的表达式;
②若D点坐标(4,0),当![]() 时,求a的取值范围.
时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】表中所列![]() 、
、![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中![]()
| … |
|
|
|
|
|
|
| … |
| … | 6 |
| 11 |
| 11 |
| 6 | … |
根据表中提供约信息,有以下4个判断:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 的值是
的值是![]() ;④
;④![]() ;其中判断正确的是( )
;其中判断正确的是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本价为50元/千克,规定每千克售价不低于成本价,且不高于85元.经过市场调查,该商品每天的销售量![]() (千克)与售价
(千克)与售价![]() (元/千克)满足一次函数关系,部分数据如下表:
(元/千克)满足一次函数关系,部分数据如下表:
售价 | 50 | 60 | 70 |
销售量 | 120 | 100 | 80 |
(1)求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.
(2)设该商品每天的总利润为![]() (元),则当售价
(元),则当售价![]() 定为多少元/千克时,超市每天能获得最大利润?最大利润是多少元?
定为多少元/千克时,超市每天能获得最大利润?最大利润是多少元?
(3)如果超市要获得每天不低于1600元的利润,且符合超市自己的规定,那么该商品的售价![]() 的取值范围是多少?请说明理由.
的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB//CD,点E是直线AB上的点,过点E的直线l交直线CD于点F,EG平分∠BEF交CD于点G.在直线l绕点E旋转的过程中,图中∠1,∠2的度数可以分别是( )
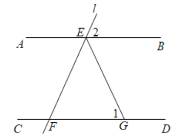
A.30°,110°B.56°,70°C.70°,40°D.100°,40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:其中,正确的个数有( )
①b2﹣4ac<0;②a﹣b+c<0;③abc>0;④m>﹣2.
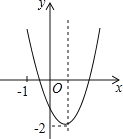
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com