
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
科目:初中数学 来源: 题型:阅读理解
|
| 1 |
| 2 |
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:022
填空题.
我国著名数学家华罗庚曾经说过这样一句话:“数形结合百般好,隔裂分家万事休”.如图,在一个边长为1的正方形纸板上,依次贴上面积为 ,
, ,
, ,
, ,…,
,…, 的小长方形纸片,请你写出最后余下未贴部分的面积的表达式:________.
的小长方形纸片,请你写出最后余下未贴部分的面积的表达式:________.

查看答案和解析>>
科目:初中数学 来源:2012年人教版七年级下第六章第二节用坐标表示地理位置练习卷(解析版) 题型:解答题
奔跑的狗
苏步青是我国著名数学家、教育家,历任复旦大家教授、校长等职.1995年当选为中国科学院学部委员.苏步青的主要研究领域是微分几何学,他又是优秀的教学教育家,从事数学教学达60年,培养了大批数学人才.
一次在德国,苏步青与一位有名的数学家同乘电车时,这位数学家出了一道题目给苏教授解答.
这道题是:
甲乙两人同时从相距100千米的两地出发,相向而行,甲每小时走6千米,乙每小时走4千米,甲带了一只狗和他同时出发,狗以每小时10千米的速度向乙奔去,遇到乙即回头向甲奔去;遇到甲又回头向乙奔去,直到甲乙两人相遇时狗才停住.问这只狗共奔跑了多少千米路?

对这个问题,苏步青教授略加思索,就算出了正确的答案.请你也想一想,该怎么解答?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
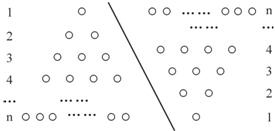
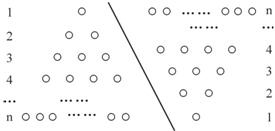
 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com