
 (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①菱形OABC的面积为80; ②E点的坐标是(4,8);③双曲线的解析式为y=
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:①菱形OABC的面积为80; ②E点的坐标是(4,8);③双曲线的解析式为y=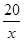 (x>0); ④
(x>0); ④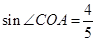 ,其中正确的结论有( )个。
,其中正确的结论有( )个。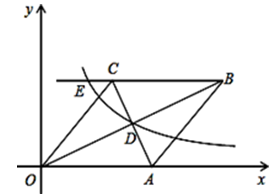
| A.1 | B.2 | C.3 | D.4 |
 (x>0)的解析式,由反比例函数的解析式与直线BC的解析式联立即可求出E点坐标;由sin∠COA=
(x>0)的解析式,由反比例函数的解析式与直线BC的解析式联立即可求出E点坐标;由sin∠COA=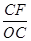 可求出∠COA的正弦值;根据A、C两点的坐标可求出AC的长,由OB•AC=160即可求出OB的长.
可求出∠COA的正弦值;根据A、C两点的坐标可求出AC的长,由OB•AC=160即可求出OB的长.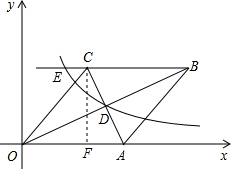
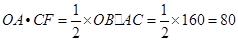 ,菱形OABC的面积为80,故①正确;
,菱形OABC的面积为80,故①正确;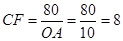
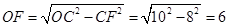 ,
,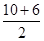 ,
,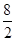 ),即(8,4),
),即(8,4), (x>0)经过D点,
(x>0)经过D点,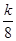 ,即k=32,
,即k=32,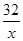 (x>0),故③错误;
(x>0),故③错误;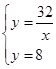 ,解得x=4,y=8,
,解得x=4,y=8,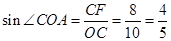 ,故④正确;
,故④正确;

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源:不详 题型:填空题
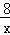 ,y2=
,y2=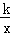 (k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k= _________ .
(k≠0)在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于点B,交y轴于点C,若S△AOB=2,则k= _________ .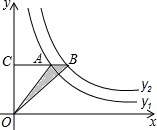
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
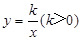 在第一象限图象上的一点,已知△P1O A1为等边三角形,点A1的坐标为(2,0).
在第一象限图象上的一点,已知△P1O A1为等边三角形,点A1的坐标为(2,0).
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
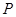 落在反比例函数
落在反比例函数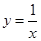 的图像上,另“7”字形有两个顶点落在
的图像上,另“7”字形有两个顶点落在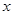 轴上,一个顶点落在
轴上,一个顶点落在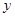 轴上.
轴上.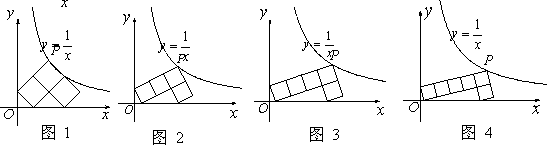
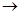 图2
图2 图3
图3 图4
图4
 这样的规律拼接下去,第
这样的规律拼接下去,第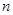 个图形中每一个小正方形的面积是 .(用含
个图形中每一个小正方形的面积是 .(用含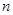 的代数式表示)
的代数式表示)查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
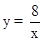 (x>0)的图象分别交于点B1,B2,B3,分别过点B1,B2,B3作x轴的平行线,分别于y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为 .
(x>0)的图象分别交于点B1,B2,B3,分别过点B1,B2,B3作x轴的平行线,分别于y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为 .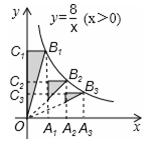
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com