
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,且AD=2,AC=BC=![]() .
.
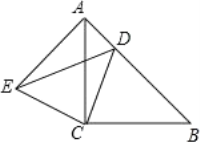
(1)证明:△ACE≌△BCD;
(2)求四边形ADCE的面积;
(3)求ED的长.
【答案】(1)见解析;(2)9;(3)![]()
【解析】
(1)根据△ACB和△ECD都是等腰直角三角形,可得:CE=CD,CA=CB,∠ECD=∠ACB=90°,再根据等式的基本性质即可得出:∠ACE=∠BCD,利用SAS即可证出△ACE≌△BCD;
(2)根据(1)中全等,四边形ADCE的面积=△ACE的面积+△ACD的面积=△BCD的面积+△ACD的面积=△ACB的面积,故计算出△ACB的面积即可;
(3)根据勾股定理即可算出AB的长,从而计算出BD的长,再根据(1)的△ACE≌△BCD即可得EA=BD,∠EAC=∠DBC=45°,从而得到∠EAD=90°,最后根据勾股定理即可算出ED的长.
解:(1)∵△ACB和△ECD都是等腰直角三角形
∴CE=CD,CA=CB,∠ECD=∠ACB=90°
∴∠ECD-∠ACD=∠ACB-∠ACD
∴∠ACE=∠BCD
在△ACE和△BCD中
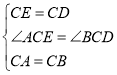
∴△ACE≌△BCD(SAS);
(2)∵△ACE≌△BCD
∴S△ACE=S△BCD
∴S四边形ADCE =S△ACE+S△ACD =S△BCD+S△ACD =S△ACB
∵AC=BC=![]()
∴S△ACB=![]()
∴S四边形ADCE =9
(3)根据勾股定理:![]()
∴BD=AB-AD=4
∵△ACE≌△BCD
∴EA=BD=4,∠EAC=∠DBC
∵△ACB是等腰直角三角形
∴∠BAC=∠DBC=45°
∴∠EAD=∠EAC+∠BAC=∠DBC+∠BAC=90°
在Rt△EAD中
根据勾股定理:![]()


科目:初中数学 来源: 题型:
【题目】等边三角形ABC 中,BD是角平分线,点E在BC边的延长线上,且CD=CE,则∠BDE的度数是( )
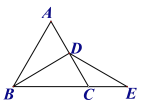
A.90°B.100°C.120°D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论: ①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)
 根据表、图提供的信息,解决以下问题:
根据表、图提供的信息,解决以下问题:
(1)计算出表中a、b的值;
(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;

(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)如图,已知△ABC,∠C=Rt∠,AC<BC,D为BC上一点,且到A,B两点的距离相等.

(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的菱形
的菱形![]() 中,对角线
中,对角线![]() ,点
,点![]() 是直线
是直线![]() 上的动点,
上的动点,![]() 于
于![]() ,
,![]() 于
于![]() .
.
如图,在边长为![]() 的菱形
的菱形![]() 中,对角线
中,对角线![]() ,点
,点![]() 是直线
是直线![]() 上的动点,
上的动点,![]() 于
于![]() ,
,![]() 于
于![]() .
.
![]() 对角线
对角线![]() 的长是________,菱形
的长是________,菱形![]() 的面积是________;
的面积是________;
![]() 如图
如图![]() ,当点
,当点![]() 在对角线
在对角线![]() 上运动时,
上运动时,![]() 的值是否发生变化?请说明理由;
的值是否发生变化?请说明理由;
![]() 如图
如图![]() ,当点
,当点![]() 在对角线
在对角线![]() 的延长线上时,
的延长线上时,![]() 的值是否发生变化?若不变请说明理由,若变化,请直接写出
的值是否发生变化?若不变请说明理由,若变化,请直接写出![]() 、
、![]() 之间的数量关系,不用明理由.
之间的数量关系,不用明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2,若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
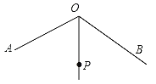
A.2个B.3个C.4个D.无数个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂里有许多剩余的三角形边角料,找出一块△ABC,测得∠C=90°(如图),现要从这块三角形上剪出一个半圆O,做成玩具,要求:使半圆O与三角形的两边AB、AC相切,切点分别为D、C,且与BC交于点E.
(1)在图中设计出符合要求的方案示意图.(要求:尺规作图,不写作法,保留作图痕迹).
(2)Rt△ABC中,AC=3,AB=5,连接AO,求出AO的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com