
【题目】如图,把长方形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置,AD与y轴交于点E,若B(4,8).
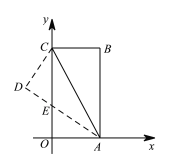
(1)△AEC是等腰三角形吗?请证明;
(2)求点D的横坐标.
【答案】(1)详见解析;(2)D(-![]() ,
,![]() ).
).
【解析】
(1)由翻折可知∠BAC=∠DAC,由OC∥AB可得∠OCA=∠BAC,所以∠EAC=∠ACE,即可证明△AEC是等腰三角形;
(2) 首先过点D作DF⊥OA于F,由四边形OABC是矩形与折叠的性质,易证得△AEC是等腰三角形,然后在Rt△AEO中,利用勾股定理求得AE,OE的长,然后等积求高法得DF的长,利用勾股定理得EF得长,即可得点D的横坐标.
⑴证明:由翻折可知,∠BAC=∠DAC,∵OC∥AB,∴∠OCA=∠BAC,
∴∠EAC=∠ACE,∴AE=CE,即△AEC是等腰三角形.
⑵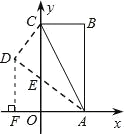
如图,过点D作DF⊥x轴于F,由(1),令AE=CE=x,则OE=8-x,
在Rt△OEA中,由勾股定理,(8-x)2+42=x2,
解得x=5,∴AE=CE=5,OE=DE=3,在Rt△CDE中,由等积求高法,得DF=![]() ,
,
利用勾股定理,EF=![]() ,于是OF=3+
,于是OF=3+![]() =
=![]() ,DF=
,DF=![]() ,
,
∴D(-![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求A,B两点间的距离(结果精确到0.1km).
(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,令
,令![]() .
.
(1)若![]() 的函数图象相交于
的函数图象相交于![]() 轴上的同一点.
轴上的同一点.
①求![]() 的值;
的值;
②当![]() 为何值时,
为何值时,![]() 的值最小,试求出该最小值.
的值最小,试求出该最小值.
(2)当![]() 时,
时,![]() 随
随![]() 的增大而减小,请写出
的增大而减小,请写出![]() 的大小关系并给予证明.
的大小关系并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形纸片ABC中,![]() ,
,![]() ,
,![]() ,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为
,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为![]() 如图
如图![]() ,剪去
,剪去![]() 后得到双层
后得到双层![]() 如图
如图![]() ,再沿着过
,再沿着过![]() 某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为______cm.
某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,
,![]() .
.
![]() 求该反比例函数和一次函数的解析式;
求该反比例函数和一次函数的解析式;
![]() 在x轴上有一点
在x轴上有一点![]() 点除外
点除外![]() ,使得
,使得![]() 与
与![]() 的面积相等,求出点E的坐标.
的面积相等,求出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:任意两个数a 、b ,按规则c = a +b-ab 扩充得到一个新数c ,称所得的新数c 为“如意数”.
(1)若a =2, b =-3,直接写出a 、b 的“如意数” c ;
(2)若a =2, b = x2 +1,求a 、b 的“如意数” c ,并比较b 与c 的大小;
(3)已知a=x2-1,且a 、b 的“如意数” c = x3 +3x2-1,则b = (用含 x 的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,超市举行有奖促销活动:凡一次性购物满300元者即可获得一次摇奖机会,摇奖机是一个圆形转盘,被分成16等分,指针分别指向红、黄、蓝色区域,分获一、二、三获奖,奖金依次为60、50、40元.
(1)分别计算获一、二、三等奖的概率.
(2)老李一次性购物满了300元,摇奖一次,获奖的概率是多少?请你预测一下老李摇奖结果会有哪几种情况?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘外卖送餐员,送餐员的月工资由底薪1000元加上外卖送单补贴![]() 送一次外卖称为一单
送一次外卖称为一单![]() 构成,外卖送单补贴的具体方案如下:
构成,外卖送单补贴的具体方案如下:
外卖送单数量 | 补贴 |
每月不超过500单 | 6 |
超过500单但不超过m单的部分 | 8 |
超过m单的部分 | 10 |
![]() 若某“外卖小哥”4月份送餐400单,则他这个月的工资总额为多少元?
若某“外卖小哥”4月份送餐400单,则他这个月的工资总额为多少元?
![]() 设5月份某“外卖小哥”送餐x单
设5月份某“外卖小哥”送餐x单![]() ,所得工资为y元,求y与x的函数关系式.
,所得工资为y元,求y与x的函数关系式.
![]() 若某“外卖小哥”5月份送餐800单,所得工资为6500元,求m的值.
若某“外卖小哥”5月份送餐800单,所得工资为6500元,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com