
【题目】正方形![]() 中,以
中,以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() ,直线
,直线![]() 交对角线
交对角线![]() 于点
于点![]() ,则
,则![]() 的度数为_______________-
的度数为_______________-
【答案】![]() 或
或![]()
【解析】
以AD为边作等边三角形,这个等边三角形可以在正方形的内部,也可以在正方形的外部,故要分类讨论并作出图形,如下图1、图2所示,然后在图1中求出∠EAB=150°,AB=AE,求出∠ABF,利用△ABF的外角定理求解;在图2中求出∠EAB=30°,AB=AE,求出∠ABE=75°,利用△ABF的外角定理求解.

解:如图1,当等边三角形ADE在正方形外部时:
∠EAB=∠DAB+∠DAE=![]() ,
,
又∵AB=AE,∴∠ABE=∠AEB=![]() ,
,
∴ 在△ABF中,由三角形外角定理知:∠BFC=∠ABE+∠BAC=![]() =60°;
=60°;
如图2,当等边三角形ADE在正方形内部时:
∠EAB=∠DAB-∠DAE=![]() ,
,
又∵AB=AE,∴∠ABE=∠AEB=![]() ,
,
∴ 在△ABF中,由三角形外角定理知:∠BFC=∠ABE+∠BAC=![]() =120°.
=120°.
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
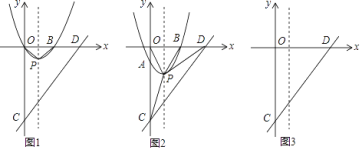
【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(1)写出点B坐标;判断△OBP的形状;
(2)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD= ![]() S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
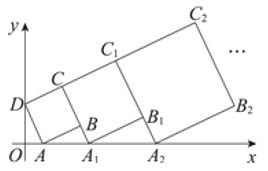
【题目】在平面直角坐标系中,正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;延长
;延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;…,按照这样的规律作正方形,则点
;…,按照这样的规律作正方形,则点![]() 的纵坐标为__________.
的纵坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级( 3 )班全体学生 2019 年初中毕业体育考试的成绩统计如下表:
成绩 | 35 | 39 | 42 | 43 | 45 | 49 | 50 |
人数 | 3 | 5 | 6 | 6 | 8 | 7 | 5 |
根据上表中的信息判断,下列结论中错误的是 ( )
A.该班一共有 40 名同学B.该班学生这次考试成绩的众数是 45 分
C.该班学生这次考试成绩的中位数是 44 分D.该班学生这次考试成绩的平均数是 45 分
查看答案和解析>>
科目:初中数学 来源: 题型:
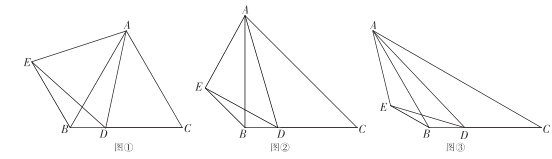
【题目】如图,在△ABC中, AB=AC,D 为 BC 边上任意一点,以AD为底边向左侧作等腰△ADE,∠AED=∠ABC ,连接![]() .
.
(1)如图 ① ,当∠ABC=60°时,易证:CD=BE(不需要证明);
(2)当∠ABC=90°时,如图 ② ;当∠ABC=120°时,如图 ③ ;线段CD和BE又有怎样的关系? 并选择一个图形证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别是A(-1,0)、B(4,5),抛物线![]() +b
+b![]() +c经过A、B两点
+c经过A、B两点
(1)求抛物线的解析式;
(2)点M是线段AB上的一点(不与A、B重合),过M作![]() 轴的垂线交抛物线与点N,求线段MN的最大值,并求出点M、N的坐标;
轴的垂线交抛物线与点N,求线段MN的最大值,并求出点M、N的坐标;
(3)在(2)的条件下,在抛物线上是否存在点P,使得⊿PMN是以MN为直角边的直角三角形?若存在求出点P的坐标,若不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
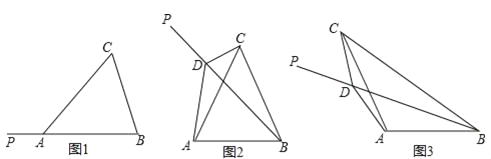
【题目】如图1,在△ABC中,AB=AC,射线BP从BA所在位置开始绕点B顺时针旋转,旋转角为α(0°<α<180°)
(1)当∠BAC=60°时,将BP旋转到图2位置,点D在射线BP上.若∠CDP=120°,则∠ACD ∠ABD(填“>”、“=”、“<”),线段BD、CD与AD之间的数量关系是 ;
(2)当∠BAC=120°时,将BP旋转到图3位置,点D在射线BP上,若∠CDP=60°,求证:BD﹣CD=![]() AD;
AD;
(3)将图3中的BP继续旋转,当30°<α<180°时,点D是直线BP上一点(点P不在线段BD上),若∠CDP=120°,请直接写出线段BD、CD与AD之间的数量关系(不必证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com