
【题目】如图,在△ABC中,点D是边BC的中点,CE∥AB,AD平分∠EAB
(1)延长AD、CE相交于点F,求证:AB=CE+AE
(2)当点E和点C重合时,试判断△ABC的形状,请画出图形,并说明理由.

【答案】(1)证明见解析;(2)等腰三角形,图形及理由见解析.
【解析】
(1)先证明△ABD≌△FCD,然后利用平行及角平分线证明AE=EF,最后结合全等的性质即可证明结论;
(2)当点E和点C重合时,AD平分∠EAB即AD平分∠CAB,然后过点D向另外两边作垂线DM和DN,证三角形△BDM和△CDN全等,得到∠B=∠C,即可得到三角形形状.
(1)证明:∵点D是边BC的中点,
∴BD=CD,
∵CE∥AB,
∴∠BAD=∠F,
在△ABD和△FCD中,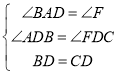 ,
,
∴△ABD≌△FCD(AAS),
∴AB=CF,
∵AD平分∠EAB,
∴∠BAD=∠DAE,
∴∠F=∠DAE,
∴AE=EF,
∵CF=CE+EF,
∴AB=CE+AE;
(2)解:△ABC为等腰三角形,图形及理由如下:
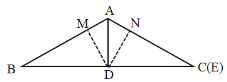
过点D作DM⊥AB,DN⊥AC,
∵AD平分∠EAB即AD平分∠CAB,且DM⊥AB,DN⊥AC,
∴DM=DN,∠DMB=∠DNC=90°,
∵点D是边BC的中点,
∴BD=CD,
在Rt△BDM和Rt△CDN中,![]() ,
,
∴Rt△BDM≌Rt△CDN(HL),
∴∠B=∠C,
∴AB=AC,即△ABC为等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,∠DAB=∠CAE,AD=AB,AC=AE.

(1)求证△ABE≌△ADC;
(2)设BE与CD交于点O,∠DAB=30°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为正方形ABCD 的中心,E为AB 边上一点,F为BC边上一点,△EBF的周长等于 BC 的长.
(1)求∠EOF 的度数.
(2)连接 OA、OC(如图2).求证:△AOE∽△CFO.
(3)若OE=![]() OF,求
OF,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
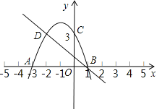
【题目】如图所示,二次函数的图象与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 、
、![]()
是二次函数图象上的一对对称点,一次函数的图象过点![]() 、
、![]() .
.
![]() 求
求![]() 点的坐标和一次函数、二次函数的解析式;
点的坐标和一次函数、二次函数的解析式;
![]() 根据图象写出使一次函数值大于二次函数值的
根据图象写出使一次函数值大于二次函数值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() 是
是![]() 边上一点(不含端点
边上一点(不含端点 ![]() ,
,![]() ),
),![]() 是
是![]() 的外角
的外角 ![]() 的平分线上一点,且
的平分线上一点,且![]() .
.

(1)尺规作图:在直线![]() 的下方,过点
的下方,过点![]() 作
作![]() ,作
,作![]() 的延长线,与
的延长线,与![]() 相交于点
相交于点![]() .
.
(2)求证:![]() 是等边
是等边![]()
(3)求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝祖国70华诞,某小区计划在一块面积为196m2的正方形空地上建一个面积为100m2的长方形花坛(长方形的边与正方形空地的边平行),要求长方形的长是宽的2倍.请你通过计算说明该小区能否实现这个愿望?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本
(1)求每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com