
 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=2,MC=6,动点P在AB边上,连接PC,PM,则PC+PM的最小值是2$\sqrt{17}$.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点M在AC边上,且AM=2,MC=6,动点P在AB边上,连接PC,PM,则PC+PM的最小值是2$\sqrt{17}$. 分析 根据平面内线段最短,构建直角三角形,解直角三角形即可.
解答  解:如图,过点作CO⊥AB于O,延长BO到C',使OC'=OC,连接MC',交AB于P,
解:如图,过点作CO⊥AB于O,延长BO到C',使OC'=OC,连接MC',交AB于P,
此时PC'=PM+PC'=PM+PC的值最小,
连接AC',
∵CO⊥AB,AC=BC,∠ACB=90°,
∴∠ACO=$\frac{1}{2}$×90°=45°,
∵CO=OC',CO⊥AB,
∴AC'=CA=AM+MC=8,
∴∠OC'A=∠OCA=45°,
∴∠C'AC=90°,
∴C'A⊥AC,
∴MC′=$\sqrt{A{M}^{2}+A{C}^{2}}$=$\sqrt{{2}^{2}+{8}^{2}}$=2$\sqrt{17}$,
∴PC+PM的最小值为2$\sqrt{17}$.
故答案为:2$\sqrt{17}$.
点评 本题考查了线路最短的问题,确定动点P为何位置时,使PC+PM的值最小是关键.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
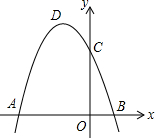 如图,抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(0,3).
如图,抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
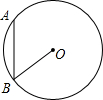 如图,AB是⊙O的弦,AB=6,OB=5,将线段AB向右侧平移,使之与圆相切,点B移至切点位置,则平移的距离为3$\sqrt{10}$.
如图,AB是⊙O的弦,AB=6,OB=5,将线段AB向右侧平移,使之与圆相切,点B移至切点位置,则平移的距离为3$\sqrt{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com