
����Ŀ����ͼ��������y��ax2+x+c��x�ύ��A��B���㣬A������Ϊ����3��0������y�ύ�ڵ�C����C����Ϊ��0����6��������BC����C����x��ĶԳƵ�D����P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
��1������κ�������ʽ��
��2����P��x�����˶�������6��m��2ʱ�����߶�MQ���ȵ����ֵ��
��3����P��x�����˶�ʱ��NΪƽ����һ�㣬ʹ�õ�B��C��M��NΪ������ı���Ϊ���Σ�������ڣ���ֱ��д����N���ꣻ�����ڣ�˵�����ɣ�

���𰸡���1��y��x2+x��6����2��MQ�����ֵΪ16����3��N����Ϊ����![]() ����
����![]() ����2��0����7.2��3.6����2����12�������ɼ�����.
����2��0����7.2��3.6����2����12�������ɼ�����.
��������
��1����A������Ϊ��-3��0������C����Ϊ��0��-6��������κ�������ʽ����ã�a=1��c=-6���ʣ����κ�������ʽΪy=x2+x-6��
��2����C����x��ĶԳƵ�D��0��6����MQ=yM-yQ=-3m+6-��m2+m-6��=-��m+2��2+16��������⣻
��3���ٵ�BC��Ϊ���εı�ʱ��N��Ӧ����x�ᣬ����B��Գƣ�����N����Ϊ��-2��0�����ڵ�BC��Ϊ���εĶԽ���ʱ����BC�Ĵ�ֱƽ����MH��ֱ��BD��ֱ��MH���㼴ΪM����Ϊ��������⣮
��1����A������Ϊ����3��0������C����Ϊ��0����6��������κ�������ʽ��
��ã�a��1��c����6��
�ʣ����κ�������ʽΪy��x2+x��6��
��2����C����x��ĶԳƵ�D��0��6����
��B��D�������ڵ�ֱ�߷���Ϊ��y����3x+6��
��M������m����3m+6������Q��m��m2+m��6����
��MQ��yM��yQ����3m+6����m2+m��6��������m+2��2+16��
�ک�6��m��2ʱ���������㴦��ȡ�����ֵ��
��MQ�����ֵΪ16��
��3���ٵ�BC��Ϊ���εı�ʱ��
���һ��N��Ӧ����x�ᣬ����B��Գƣ�����N����Ϊ����2��0����
�������BC��MB�����������ڱߣ���BC��BM�����N����Ϊ��2����12����
�������BC��CMΪ�ڱ�ʱ�����N����Ϊ��7.2��3.6����
�ڵ�BC��Ϊ���εĶԽ���ʱ����BC�Ĵ�ֱƽ����MH��
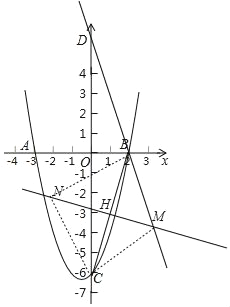
��ֱ��DB��MH�Ľ���ΪM��M����BC�ĶԳƵ�ΪN��HΪBC���е㣬
��H������1����3����
ֱ��BD�ķ���Ϊ��y����3x+6��ֱ��MH�ķ���Ϊ��y=-![]() x-
x-![]() ��
��
���������������̣���ã�M����Ϊ��![]() ����
����![]() ����
����
ͬ����N����Ϊ����![]() ����
����![]() ����
����
�ʣ�N����Ϊ����![]() ����
����![]() ����2��0����7.2��3.6����2����12����
����2��0����7.2��3.6����2����12����


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
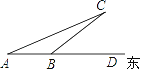
����Ŀ����ͼ��һ���ִ���18����/ʱ���ٶ��������У���A�����С��C�ڱ�ƫ��75�������ϣ���Сʱ���ִ���B�����С��C�ڱ�ƫ��60�������ϣ���С����Χ15���ﴦ�а��������ִ���Ȼ��18����/ʱ���ٶ����У������Ƿ��д���Σ�գ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ĸ�С�������ֱ����2��3��4��6�ĸ����֣����ǵIJ��ʡ���״����С��ȫ��ͬ�������������һ��С���������Ϊx���ٴ�ʣ�µ����������������һ�����������Ϊy����A������Ϊ��x,y).���û���״ͼ���б��ķ�����д��A�����п��ܵ����꣬�������A�ڷ���������![]() ͼ���ϵĸ���.
ͼ���ϵĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ�����ͼ����x�ύ��A����2��0����B��4��0�����㣬�Һ��������㣨3��10����
��1������κ����Ľ���ʽ��
��2����������κ����Ķ���ΪP������ABP�������
��3����xΪ��ֵʱ��y��0������ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
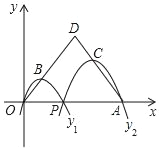
����Ŀ����ͼ����֪��AOD�ǵ��������Σ���A��12��0����OΪ����ԭ�㣬P���߶�OA������һ�㣨�����˵�O��A������P��O����Ķ��κ���y1����P��A����Ķ��κ���y2���Ŀ��ھ����£����ǵĶ���ֱ�ΪB��C����B��C�ֱ���OD��AD�ϣ���OD=AD=10ʱ�����������κ��������ֵ֮�͵���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
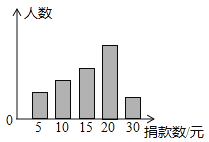
����Ŀ��������ѧУѧ����ɲ���Уѧ���ᳫ��������������Ը������г����������õ�һ��ѧ������������������ͼ�Ǹ����������ݻ��Ƶ�ͳ��ͼ��ͼ�д����Ҹ������θ߶�֮��Ϊ3��4��5��8��2����֪�˴ε����о�15Ԫ��20Ԫ��������39����
��1������һ������˶����ˣ�
��2������У����2310��ѧ���������ȫУѧ����������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90����AC=4��BC=3��O����ABC�����ģ���OΪԲ�ģ�rΪ�뾶��Բ���߶�AB�н��㣬��r��ȡֵ��Χ�ǣ� ��
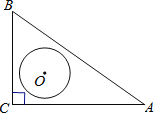
A��r��1 B��1��r��![]() C��1��r��
C��1��r��![]() D��1��r��4
D��1��r��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
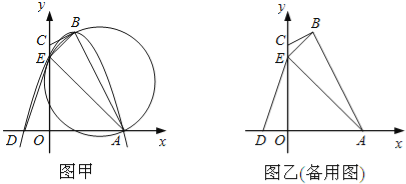
����Ŀ����ͼ�ף��ı���OABC�ı�OA��OC�ֱ���x�ᡢy����������ϣ�������B��������߽�x���ڵ�A��D����y���ڵ�E������AB��AE��BE����֪tan��CBE=![]() ��A��3��0����D����1��0����E��0��3����
��A��3��0����D����1��0����E��0��3����
��1���������ߵĽ���ʽ������B�����ꣻ
��2����֤��CB����ABE���Բ�����ߣ�
��3����̽�����������Ƿ����һ��P��ʹ��D��E��PΪ���������������ABE���ƣ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
��4������AOE��x��������ƽ��t����λ���ȣ�0��t��3��ʱ����AOE����ABE�ص����ֵ����Ϊs����s��t֮��ĺ�����ϵʽ����ָ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���֪��B������Ϊ��6��4����
��1������ֱ�ߣ������̶ȣ���Բ����һ��ֱ��AC������x���y���������ֱ��ڵ�A�͵�C����ʹ��ABC=90�㣬��ABC����AOC�������ȣ�����ͼ����д��������Ҫ������ͼ�ۼ�����
��2���ʣ���1����������ֱ��AC�Ƿ�Ψһ����Ψһ����˵�����ɣ�����Ψһ������ͼ�л�������������ֱ��AC����д����֮��Ӧ�ĺ�������ʽ��
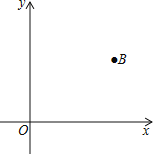
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com