
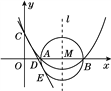
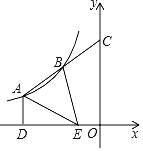
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
【答案】 (1) y=![]() x2-
x2-![]() x+2,A(2,0),B(6,0).(2)存在,AP+CP的最小值为2
x+2,A(2,0),B(6,0).(2)存在,AP+CP的最小值为2![]() ;(3)直线CE的表达式为y=-
;(3)直线CE的表达式为y=-![]() x+2.
x+2.
【解析】试题分析:(1)根据知抛物线的顶点坐标,设抛物线的解析式为y=a(x﹣4)2﹣![]() ,再根据抛物线经过(0,2)求出抛物线解析式,进而求出A、B两点的坐标;(2)存在,线段BC的长即为AP+CP的最小值,求得BC的长即可;(3)连接ME,根据已知条件易证△COD≌△MED.根据全等三角形的性质可得OD=DE,DC=DM.设OD=x,则CD=DM=OM-OD=4-x.在Rt△COD中,根据勾股定理列出方程x2+22=(4-x)2.解方程求得x的值,即可得点D的坐标,利用待定系数法求得直线EC的解析式即可
,再根据抛物线经过(0,2)求出抛物线解析式,进而求出A、B两点的坐标;(2)存在,线段BC的长即为AP+CP的最小值,求得BC的长即可;(3)连接ME,根据已知条件易证△COD≌△MED.根据全等三角形的性质可得OD=DE,DC=DM.设OD=x,则CD=DM=OM-OD=4-x.在Rt△COD中,根据勾股定理列出方程x2+22=(4-x)2.解方程求得x的值,即可得点D的坐标,利用待定系数法求得直线EC的解析式即可
试题解析:
(1)由题意可设抛物线的表达式为y=a(x-4)2-![]() (a≠0).
(a≠0).
∵抛物线经过点C(0,2),
∴a(0-4)2-![]() =2,
=2,
解得a=![]() .
.
∴y=![]() (x-4)2-
(x-4)2-![]() ,
,
即y=![]() x2-
x2-![]() x+2.
x+2.
当y=0时,![]() x2-
x2-![]() x+2=0,
x+2=0,
解得x1=2,x2=6,
∴A(2,0),B(6,0).
(2)存在,由(1)知,抛物线的对称轴l为直线x =4.
∵A,B两点关于l对称,
连接CB交l于点P,连接AP,则AP=BP,
∴AP+CP=BC的值最小.
∵B(6,0),C(0,2),
∴OB=6,OC=2.
∴BC=![]() =2
=2![]() .
.
∴AP+CP=BC=2![]() .
.
∴AP+CP的最小值为2![]() .
.
(3)连接ME,∵CE是⊙M的切线,
∴CE⊥ME.
∴∠CEM=90°.
∴∠COD=∠DEM=90°.
由题意,得OC=ME=2,
∠ODC=∠MDE,
∴△COD≌△MED.
∴OD=DE,DC=DM.
设OD=x,
则CD=DM=OM-OD=4-x.
在Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4-x)2.
∴x=![]() .
.
∴D![]() .
.
设直线CE的表达式为y=kx+d(k≠0),
∵直线CE过C(0,2),
D![]() 两点,
两点,
则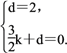
解得
∴直线CE的表达式为y=-![]() x+2.
x+2.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是16cm,AC的长为8cm,求线段AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 点是第二象限内一点,
点是第二象限内一点,![]() 轴于
轴于![]() ,且
,且![]() 是
是![]() 轴正半轴上一点,
轴正半轴上一点,![]() 是x轴负半
是x轴负半![]() 轴上一点,且
轴上一点,且![]() .
.

(1)![]() ( ),
( ),![]() ( )
( )
(2)如图2,设![]() 为线段
为线段![]() 上一动点,当
上一动点,当![]() 时,
时,![]() 的角平分线与
的角平分线与![]() 的角平分线的反向延长线交于点
的角平分线的反向延长线交于点![]() ,求
,求![]() 的度数: (注: 三角形三个内角的和为
的度数: (注: 三角形三个内角的和为![]() )
)
(3)如图3,当![]() 点在线段
点在线段![]() 上运动时,作
上运动时,作![]() 交
交![]() 于
于![]() 的平分线交于
的平分线交于![]() ,当
,当![]() 点在运动的过程中,
点在运动的过程中,![]() 的大小是否变化?若不变,求出其值;若变化,请说明理由.
的大小是否变化?若不变,求出其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐红萝卜,以每筐25千克为标准,超过记正不足记负来表示,记录如下:

(1)20筐红萝卜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准质量比较,20筐红萝卜总计超过或不足多少千克?
(3)若该种红萝卜进价每千克为1.5元,售价每千克为3元.求这20筐红萝卜能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
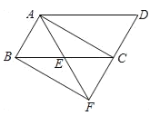
【题目】已知:如图,在□ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,判断四边形ABFC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
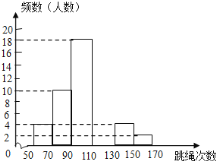
(1)a= ,b= ;
(2)这个样本数据的中位数落在第 组;
(3)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少;
(4)若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
组别 | 次数x | 频数(人数) |
第1组 | 50≤x<70 | 4 |
第2组 | 70≤x<90 | a |
第3组 | 90≤x<110 | 18 |
第4组 | 110≤x<130 | b |
第5组 | 130≤x<150 | 4 |
第6组 | 150≤x<170 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下列的相似测试.
如图,在△ABC中,AB=AC=4,D是AB上一点,且BD=1,连接CD,然后作∠CDE=∠B,交平行于BC且过点A的直线于点E,DE交AC于点F,连接CE.
(1)求证:△AFD∽△EFC;
(2)试求AEBC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABE中,点A、B是反比例函数y=![]() (k≠0)图象上的两点,点E在x轴上,延长线段AB交y轴于点C,点B恰为线段AC中点,过点A作AD⊥x轴于点D.若S△ABE=
(k≠0)图象上的两点,点E在x轴上,延长线段AB交y轴于点C,点B恰为线段AC中点,过点A作AD⊥x轴于点D.若S△ABE=![]() ,DE=2OE,则k的值为( )
,DE=2OE,则k的值为( )
A.6B.﹣6C.9D.﹣9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com