
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为12,则k的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为12,则k的值为( )| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
分析 本题可从反比例函数图象上的点E、M、D入手,分别找出△OCE、△OAD、□OABC的面积与|k|的关系,列出等式求出k值.
解答 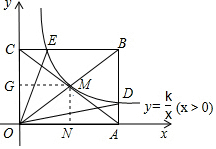 解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=$\frac{1}{2}$|k|,S△OAD=$\frac{1}{2}$|k|,
解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=$\frac{1}{2}$|k|,S△OAD=$\frac{1}{2}$|k|,
过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,
又∵M为矩形ABCO对角线的交点,则S矩形ABCO=4S□ONMG=4|k|,
由于函数图象在第一象限,
∴k>0,则$\frac{k}{2}$+$\frac{k}{2}$+12=4k,
∴k=4.
故选B.
点评 本题考查了反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|.本知识点是中考的重要考点,同学们应高度关注.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:解答题
 跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.
跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 6个 | D. | 7个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
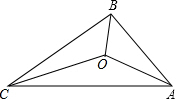 如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )
如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S△OAB:S△OBC:S△OAC=( )| A. | 1:1:1 | B. | 1:2:3 | C. | 2:3:4 | D. | 3:4:5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com