Question

10．已知：如图1，△ABC中，点P，Q分别是∠BAC的平分线AD，边AB上的两个动点，∠C=α，BC=6．
（1）若α=45°，求PB+PQ的最小值．
（2）若α=70°，求PB+PQ的最小值．
（3）若α=90°，如图2，点E在边AB上，且AE=2EB，求PE+PQ的最小值．

Answer 1

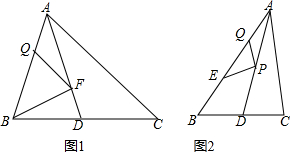
分析 （1）先判断出PB+PQ的最小值时，点M的位置，得出最小值就出BM，利用三角函数求出BM；
（2）同（1）即可得出结果；
（3）作图同（1），由平行线分线段成比例定理求出EM即可．

解答 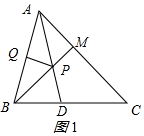解：（1）如图1作出点Q关于AD的对称点M，
∵AD是∠BAC的平分线，
∴点M在边AC上，
连接BM交AD于P，
当BM⊥AB时，PB+PQ的最小值是BM．
∵∠C=45°，BC=6，
∴BM=BC•sin45°=6×$\frac{\sqrt{2}}{2}$=3$\sqrt{2}$；
即若α=45°，PB+PQ的最小值为3$\sqrt{2}$．
（2）同（1）得：若α=70°，PB+PQ的最小值为6sin70°．
（3）作点Q关于AD的对称点M，连接EM交AD于P，
当EM⊥AC时，PE+PQ的最小值是EM，
则EM∥BC，
∵AE=2EB，
∴$\frac{EM}{BC}$=$\frac{2}{3}$，
∴EM=$\frac{2}{3}$BC=$\frac{2}{3}$×6=4，
即PE+PQ的最小值为4．

点评 此题是三角形综合题目，考查了轴对称-最短路线问题，主要考查了角平分线的性质，对称的性质，勾股定理，等面积法；本题综合性强，有一定难度．