
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
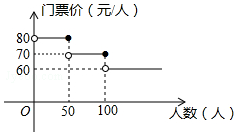 我市某风景区门票价格如图所示,某旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
我市某风景区门票价格如图所示,某旅行社有甲、乙两个旅行团队,计划在“五一”小黄金周期间到该景点游玩,两团队游客人数之和为120人,乙团队人数不超过50人.设甲团队人数为x人,如果甲、乙两团队分别购买门票,两团队门票款之和为W元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
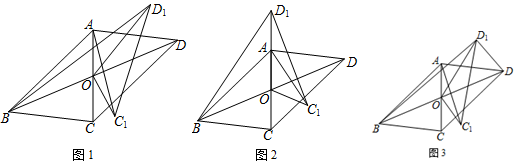
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com