
已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE、BD.
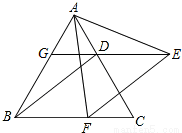
(1)求证:△AGE≌△DAB;
(2)过点E作EF∥DB,交BC于点F,连接AF,求∠AFE的度数.
(1)证明见解析;(2)60°.
【解析】
试题分析:(1)根据SAS判定△AGE和△DAB全等;
(2)证明四边形DEFB是平行四边形,△AEF是个等边三角形.
试题解析:(1)证明:∵△ABC是等边三角形,DG∥BC,
∴∠AGD=∠ABC=60°,∠ADG=∠ACB=60°,且∠BAC=60°,
∴△AGD是等边三角形,
AG=GD=AD,∠AGD=60°.
∵DE=DC,∴GE=GD+DE=AD+DC=AC=AB,
∴在△AGE与△DAB中,

∴△AGE≌△DAB(SAS);
(2)【解析】
由(1)知AE=BD,∠ABD=∠AEG.
∵EF∥DB,DG∥BC,
∴四边形BFED是平行四边形.
∴EF=BD,
∴EF=AE.
∵∠DBC=∠DEF,
∴∠ABD+∠DBC=∠AEG+∠DEF,即∠AEF=∠ABC=60°.
∴△AFE是等边三角形,∠AFE=60°.
考点:1.全等三角形的判定;2.等边三角形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年云南省八年级上学期期末考试数学试卷(解析版) 题型:解答题
(1)因式分【解析】
x3+2x2y+xy2.
(2)化简 (a+b)2-(a-b)2
(3)计算: 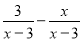
(4)计算: 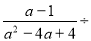
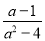
(5)计算: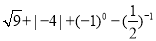
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省七年级上学期12月月考数学试卷(解析版) 题型:解答题
(本小题8分)如图,已知点A、B、C是数轴上三点,点C表示的数为6,BC=4,AB=12.

(1)数轴上点A表示的数是 ,点B表示的数是 ;
(2)动点P、Q同时从A、C出发,点P以每秒6个单位长度的速度沿数轴向右匀速运动,点Q以3个单位长度的速度沿数轴向左匀速运动,M为AP的中点, N在线段CQ上,且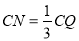 ,设运动时间为t(t>0)秒.
,设运动时间为t(t>0)秒.
①求数轴上点M、N表示的数(用含t的式子表示);
②t为何值时,原点O恰为线段PQ的中点.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省七年级上学期12月月考数学试卷(解析版) 题型:选择题
长方体的截面中边数最多的多边形是 ( )
A.四边形 B.五边形 C.六边形 D.七边形
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(云南昆明卷)数学(解析版) 题型:解答题
(6分)(2014•昆明)九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一样),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com